P14718 [RMI 2025] 松鼠 / Squirrel
题目描述
一只松鼠发现了一个存放坚果的储藏室。
储藏室包含 $N$ 行房间,编号从 $0$ 到 $N-1$。
索引为 $i$ 的一行包含 $i+1$ 个房间,编号从 $0$ 到 $i$。
位于第 $i$ 行第 $j$ 列的房间包含 $A_{ij}$ 个坚果。
在 $\frac{N \times (N+1)}{2}$ 个房间中,数 $A_{ij}$ 两两不同,且取值在 $1$ 到 $\frac{N \times (N+1)}{2}$ 之间。
形式化地说,储藏室的形状是一个三角形半矩阵,即主对角线下方(包含主对角线)的那一部分,其中每个元素表示坚果数量。
这个半矩阵中的数是从 $1$ 到 $\frac{N \times (N+1)}{2}$ 的所有整数,每个数恰好出现一次。
例如,当 $N = 5$ 时,储藏室会有 15 个房间,包含从 1 到 15 的数字。
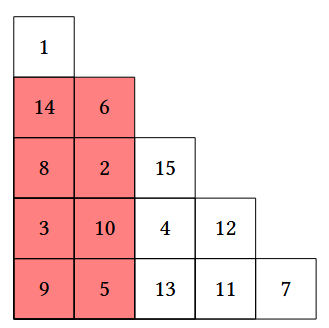
这种储藏室的一个例子可以是下面所示的半矩阵:
::::align{center}
::::
松鼠沿着主对角线行走,并且在位于 $(i, i)$ 的每个房间,它会选择一个位于以 $(i, i)$ 为右上角、以 $(N-1, 0)$ 为左下角的矩形中的房间,并吃掉该房间里的橡实。
在上面的例子中,当松鼠位于 $(1, 1)$ 时,它可以选择吃掉红色标出的 8 个房间中的任意一个房间里的坚果。
当它走过主对角线上的所有房间并且恰好吃了 $N$ 个不同房间里的坚果后,松鼠心满意足地离开。
要求:给定 $N$ 以及对任意 $0 \le i < N$ 和 $0 \le j \le i$ 的 $A_{ij}$,求松鼠最多能吃到多少坚果。
同时,对于它访问的 $N$ 个房间中的每一个,求松鼠所吃的坚果数量。
### 实现细节
这是一道(函数式)交互题。你不需要,也不应该定义 `main` 函数。
你需要实现函数
```cpp
void solve(int N, vector A, long long& answer, vector& solution)
```
函数参数:
输入数据:
* `int N`:储藏室大小 / 行数
* `vector A`:每个房间中的坚果数量(更准确地说,在 $A_{ij}$ 中,$0 \le i < N$ 且 $0 \le j \le i$,你会找到第 $i$ 行第 $j$ 个位置的房间中的坚果数量)
输出数据:
* `long long &answer`:将包含松鼠走过对角线上的全部 $N$ 个房间后能够吃到的最大坚果数量。
* `vector &solution`:一个 `vector`,包含松鼠在每个房间中吃到的坚果数量。(更准确地说,$solution_i$ 且 $0 \le i < N$ 表示松鼠位于房间 $(i,i)$ 时吃到的坚果数量)
**注意**:对于 $A$ 和 $solution$,下标从 $0$ 开始,并且 $solution$ 的大小应当恰好为 $N$。
输入格式
见「实现细节」。
输出格式
见「实现细节」。
说明/提示
### 约束
* $1 \le N \le 2000$
* $1 \le A_{ij} \le \frac{N \times (N+1)}{2}$
| # | 分数 | 约束 |
|:-:|:-:|:-:|
| $1$ | $11$ | $N \le 5$ |
| $2$ | $12$ | $N \le 100$ |
| $3$ | $23$ | $N \le 500$ |
| $4$ | $15$ | $N \le 1000$ |
| $5$ | $13$ | $N \le 1200$ |
| $6$ | $8 $ | 矩阵的内容是随机分配的。 |
| $7$ | $18$ | 无额外约束 |