P14720 [RMI 2025] 鼠皇 / King of rats
题目描述
给定正整数 $n,k$。
考虑一个 $2$ 行 $n$ 列的网格图,其中每个格子上填写着 $0$ 或 $1$。图上共有 $k$ 个 $1$。
定义两个格子相连,当且仅当它们共享一条公共边。
在所有符合条件的图等概率出现的前提下,求出这张图上所有填写着 $1$ 的格子的期望连通分量个数,答案对 $998\, 244\, 353$ 取模。
### 实现
你需要实现以下函数:
```cpp
void prec(int subtask_id)
```
```cpp
int solve(int n, int k)
```
第一个函数会在评测程序开始时被调用一次,你可以用它来做预处理。
第二个函数应当在给定参数 $n$ 和 $k$ 的情况下,返回危险度的期望值,对模数 $998\,244\,353$ 取模。
形式化地,设 $M = 998\,244\,353$ 。可以证明答案可以表示为既约分数 $\frac{p}{q}$,其中 $p$ 和 $q$ 是整数且 $q \neq 0 \pmod M$。
返回等于 $p \cdot q^{-1} \pmod M$ 的整数。
换句话说,返回一个整数 $x$,满足 $0 \le x < M$ 且 $x \cdot q \equiv p \pmod M$。
第二个函数将会被调用 $t$ 次。也就是说,输入中包含多组测试数据!
输入格式
见「实现细节」。
输出格式
见「实现细节」。
说明/提示
注意,评测程序会被提供子任务编号、测试数据组数 $t$,以及每组测试数据对应的 $n, k$ 的值。
### 样例解释
对于第一个样例的第一组测试数据,所有可能的配置如下所示:
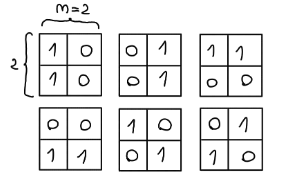
一共有 6 种配置,其中有 4 种只有一个连通分量。
因此答案为 $\frac{4 \cdot 1 + 2 \cdot 2}{6} = \frac{4}{3}$。
### 约束
* $1 \le t \le 10$
* $1 \le n \le 10^9$
* $0 \le k \le 10^6$
* $k \le 2 \cdot n$
| # | 分值 | 约束条件 |
|:---:|:------:|----------|
| $1$ | $10$ | $1 \le n \le 100$ |
| $2$ | $5 $ | $1 \le n \le 2000$ |
| $3$ | $5 $ | $k \le 3$ |
| $4$ | $15$ | $k \le 40$ |
| $5$ | $10$ | $k \le 400$ |
| $6$ | $15$ | $k \le 2000$ |
| $7$ | $40$ | 无额外限制 |