P14723 [ICPC 2022 Seoul R] Castle Design

The ICPC kingdom has decided to build a new castle. The boundary of the castle is designed as a **rectilinear polygon** with edges parallel to the $x$-axis or to the $y$-axis. To minimize the damage exposed by the enemy attack, the kingdom wants to minimize the perimeter of the rectilinear polygon. Let us go into more detail. A rectilinear polygon $P$ of $n$ vertices with integer coordinates realizes a **turn sequence** $S$ of length $n$ of two letters L and R if there is a counterclockwise traverse along the boundary of $P$ such that the turns at vertices of $P$, encountered during the traverse, form the turn sequence $S$; the left turn at a convex vertex corresponds to L and the right turn at a reflex vertex corresponds to R. For example, the rectilinear polygon in Figure B.1(a) realizes the turn sequence $S = \text{RLLRLLLLRRLRIRLLL}$ of length 16. Another turn sequence $S = \text{LLRLLRLLRLLRLLR}$ of length 14 can be realized by rectilinear polygons in Figure B.1(b) and B.1(c). Note that a turn sequence can have infinitely many realizations of rectilinear polygons in the integral plane. A polygon is **simple** if there are no two edges that intersect except at the end vertices of adjacent edges. A polygon is **monotone** to an axis if its intersection with a line orthogonal to the axis is at most one segment. The monotone polygon is called **2-monotone** if it is monotone to both $x$-axis and the $y$-axis, and **1-monotone** if it is monotone to the one axis but not to the other axis. For example, the polygon in Figure B.1(a) is 1-monotone because it is monotone to only one axis, the $x$-axis, while the polygons in Figure B.1(b) and B.1(c) are 2-monotone. A turn sequence is also said to be **$t$-monotone** if any simple rectilinear polygon realizing the turn sequence is $t$-monotone where $t = 1, 2$. 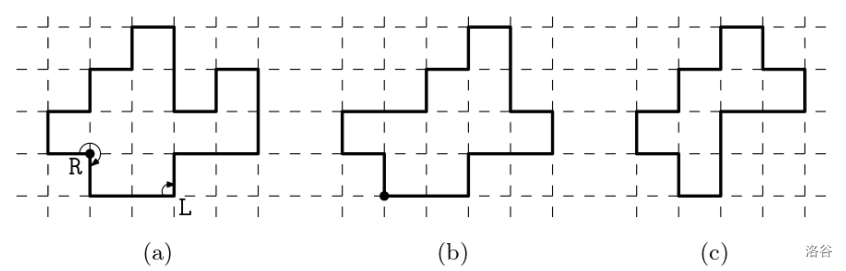:::align{center}  Figure B.1 (a) A simple 1-monotone rectilinear polygon realizing a 1-monotone turn sequence RLLRLLLRRLLRIRLLL (starting from the marked vertex). (b) A simple 2-monotone rectilinear polygon realizing a 2-monotone turn sequence LLRLLRLLRLLRLLR (starting from the marked vertex). (c) The 2-monotone rectilinear polygon with the minimum perimeter for the turn sequence in (b). ::: The perimeter of a rectilinear polygon is the sum of the length of its edges. The perimeter of the polygon in Figure B.1(b) is 18, but this is not minimum for `LLRLLRLLRLLRLLR`. Its minimum perimeter should be 16 as in Figure B.1(c). Given a $t$-monotone turn sequence of $n$ turns for $t = 1, 2$, write a program to compute the minimum perimeter of simple $t$-monotone rectilinear polygons that realize the input $t$-monotone turn sequence.

Your program is to read from standard input. The input is one line containing a string of $n$ turns of two uppercase letters L and R that is a $t$-monotone turn sequence, where $t = 1, 2$ and $4 \leq n \leq 10^{t+3}$.

Your program is to write to standard output. Print exactly one line. The line should contain the positive integer that is the minimum perimeter of simple $t$-monotone rectilinear polygons that realize the input $t$-monotone turn sequence for $t = 1, 2$.