P14724 [ICPC 2022 Seoul R] Empty Quadrilaterals

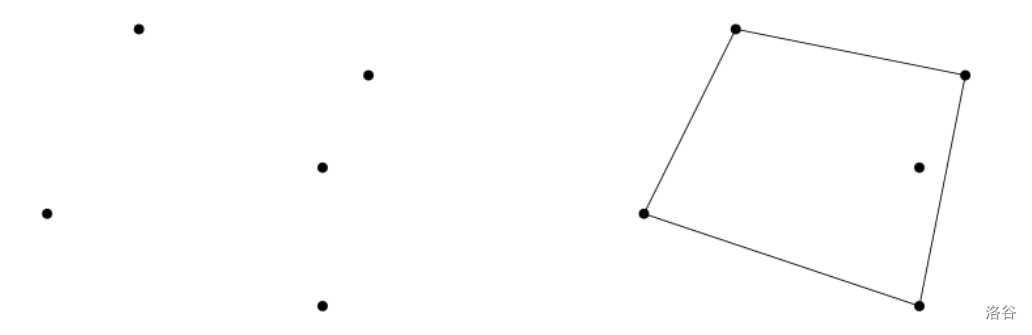
一个**四边形**是一个恰好有四个不同顶点和四条不同边的多边形，且其边之间没有任何交叉。在本问题中，给定平面上 $n$ 个点的集合 $P$，其中任意三点不共线，要求计算所有满足以下条件的四边形的数量：其顶点是集合 $P$ 中的点，并且其内部不包含 $P$ 中的任何其他点。 :::align{center}  ::: 例如，假设 $P$ 由如上图左侧所示的五个点组成。总共有九个不同的四边形，其顶点都是 $P$ 中的点，但其中只有一个四边形的内部包含 $P$ 中的一个点，如上图右侧所示。因此，恰好有八个四边形满足条件，你的程序必须输出 $8$ 作为正确答案。

你的程序需要从标准输入读取数据。输入的第一行包含一个整数 $n$ ($1 \leq n \leq 300$)，其中 $n$ 表示集合 $P$ 中的点数。接下来的 $n$ 行，每行包含两个整数，范围从 $-10^9$ 到 $10^9$，表示 $P$ 中一个点的坐标。保证 $P$ 中不存在三点共线。

你的程序需要向标准输出写入数据。输出恰好一行，包含一个整数，表示满足条件的四边形的数量：其顶点是集合 $P$ 中的点，且其内部不包含 $P$ 中的任何其他点。

翻译由 DeepSeek V3 完成