P14726 [ICPC 2022 Seoul R] Forbidden Turns

一家 GPS 导航公司 ICPC（国际精准控制公司）为交通网络设计了一套汽车导航系统。该系统将交通网络抽象为一个有向图 $G(V, E)$，其中边具有成本 $c$。对于一条有向边 $(v, w) \in E$，$c(v, w)$ 表示从地点 $v \in V$ 到另一地点 $w \in V$ 的距离。公司希望在系统中实现最短路径模块。为了反映交通网络交叉路口处某些转向通常不允许的现实情况，我们希望找到一条不包含被禁止转向作为子路径的最短路径。 从 $v$ 到 $w$ 的一条路径是一个顶点序列 $(v_1, v_2, \cdots, v_k)$，其中 $v_1 = v$，$v_k = w$，且 $(v_i, v_{i+1}) \in E$ 对于 $1 \leq i \leq k-1$。与路径的常见定义不同，这里允许在一条路径中重复访问相同的顶点一次或多次。路径的一个**子路径**是对应该序列的一个连续子序列。一个**被禁止的转向**是一条路径（即三元组）$(x, y, z)$，满足 $x, y, z \in V$ 且 $(x, y) \in E$ 和 $(y, z) \in E$。一条路径 $(v_1, v_2, \cdots, v_k)$ 的距离定义为 $\sum_{i=1}^{k-1} c(v_i, v_{i+1})$。从 $v \in V$ 到 $w \in V$ 的**最短路径**是一条从 $v$ 到 $w$ 且具有最小距离的路径。公司希望找到两个指定顶点之间避免所有被禁止转向的最短路径的距离。注意，从 $v \in V$ 到 $v \in V$ 的最短路径距离为 $0$，并且它避开了所有被禁止的转向。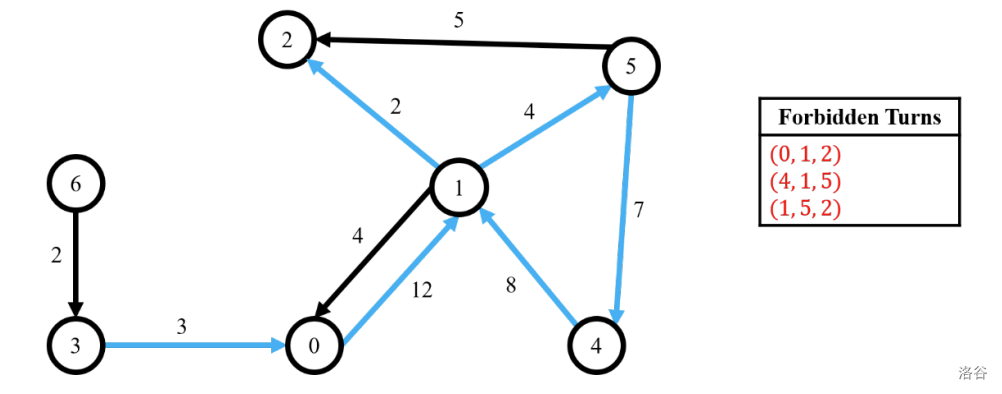 请看下图的示例。每条边的成本标注在边旁，三个被禁止转向的列表在右侧框中。从顶点 $3$ 到顶点 $2$ 的不包含被禁止转向的最短路径是 $(3, 0, 1, 5, 4, 1, 2)$，在下图中用蓝色箭头表示。该最短路径的距离为 $3 + 12 + 4 + 7 + 8 + 2 = 36$。注意，我们不能采用更短的路径 $(3, 0, 1, 2)$ 和 $(3, 0, 1, 5, 2)$，因为它们分别包含被禁止转向 $(0, 1, 2)$ 和 $(1, 5, 2)$。 :::align{center}  ::: 给定一个有向图 $G(V, E)$ 及其边成本 $c$、一个被禁止转向的集合 $F$ 以及两个顶点 $v$ 和 $w$，请编写一个程序，输出从 $v$ 到 $w$ 的、避开所有被禁止转向的最短路径的距离。我们假设每个顶点 $v$ 的出度（即从 $v$ 出发的边的数量）最多为 $10$。

你的程序需要从标准输入读取数据。输入的第一行包含三个整数 $m$、$n$ 和 $k$（$0 \leq m \leq 10n$， $1 \leq n \leq 30,000$， $0 \leq k \leq 500,000$），其中 $m$ 是有向边的数量，$n$ 是顶点数量，$k$ 是给定有向图 $G(V, E)$ 中被禁止转向的数量。这里，$k$ 小于等于给定有向图 $G(V, E)$ 中所有可能的被禁止转向的数量。顶点编号从 $0$ 到 $n-1$。第二行包含两个整数 $v$ 和 $w$，分别表示源点和目标顶点。接下来的 $m$ 行中，第 $i$ 行包含三个整数 $x_i$、$y_i$ 和 $c_i$ ($0 \leq x_i \ne y_i \leq n-1$ 且 $0 \leq c_i \leq 10^3$)，分别表示一条边 $(x_i, y_i) \in E$ 及其成本。接下来的 $k$ 行中，第 $i$ 行包含三个整数 $x_i$、$y_i$ 和 $z_i$，表示一个被禁止转向 $(x_i, y_i, z_i)$。

你的程序需要向标准输出写入数据。输出恰好一行。该行应包含一个整数，表示从 $v$ 到 $w$ 的、避开所有被禁止转向的最短路径的距离。如果这样的路径不存在，则该行应包含 $-1$。

翻译由 DeepSeek V3 完成