P14735 [ICPC 2021 Seoul R] Double Rainbow

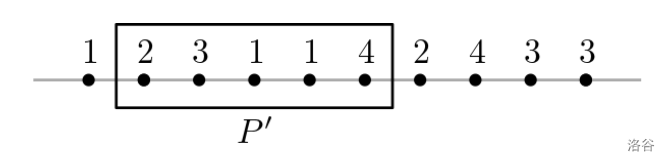
设 $P$ 是 $x$ 轴上 $n$ 个点的集合，每个点被染成 $k$ 种颜色 $1, 2, \ldots, k$ 中的一种。对于 $k$ 种颜色中的每种颜色 $i$，$P$ 中至少有一个点被染成颜色 $i$。对于 $P$ 的一个连续点子集 $P'$，如果 $P'$ 和 $P \setminus P'$ 都包含每种颜色的至少一个点，那么我们称 $P'$ 构成一个 **双彩虹**。请参见下图作为示例。集合 $P$ 包含十个点，每个点被染成颜色 $1$、$2$、$3$、$4$ 之一。矩形中包含的五个连续点组成的集合 $P'$ 构成了一个双彩虹。 :::align{center}  ::: 给定点集 $P$ 和颜色数量 $k$ 作为输入，请编写一个程序，计算并输出构成双彩虹的 $P'$ 的最小大小。

你的程序需要从标准输入读取数据。输入的第一行包含两个整数 $n$ 和 $k$ ($1 \leq k \leq n \leq 10,000$)，其中 $n$ 是 $P$ 中点的数量，$k$ 是颜色的数量。接下来的 $n$ 行每行包含一个 $1$ 到 $k$（含）之间的整数，第 $i$ 行对应于 $P$ 中从左数第 $i$ 个点的颜色。

你的程序需要向标准输出写入数据。输出恰好一行。该行应包含构成双彩虹的 $P'$ 的最小大小。如果不存在这样的 $P'$，则输出 $0$。

翻译由 DeepSeek V3 完成