P14735 [ICPC 2021 Seoul R] Double Rainbow

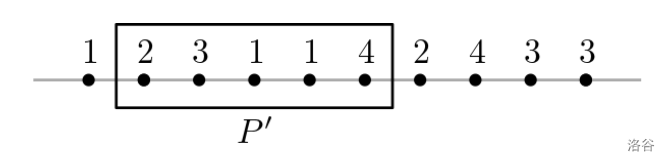
Let $P$ be a set of $n$ points on the x-axis and each of the points is colored with one of the colors $1, 2, \ldots, k$. For each color $i$ of the $k$ colors, there is at least one point in $P$ which is colored with $i$. For a set $P'$ of consecutive points from $P$, if both $P'$ and $P \setminus P'$ contain at least one point of each color, then we say that $P'$ makes a **double rainbow**. See the below figure as an example. The set $P$ consists of ten points and each of the points is colored by one of the colors $1, 2, 3$, and $4$. The set $P'$ of the five consecutive points contained in the rectangle makes a double rainbow. :::align{center}  ::: Given a set $P$ of points and the number $k$ of colors as input, write a program that computes and prints out the minimum size of $P'$ that makes a double rainbow.

Your program is to read from standard input. The input starts with a line containing two integers $n$ and $k$ ($1 \leq k \leq n \leq 10,000$), where $n$ is the number of the points in $P$ and $k$ is the number of the colors. Each of the following $n$ lines consists of an integer from $1$ to $k$, inclusively, and the $i$-th line corresponds to the color of the $i$-th point of $P$ from the left.

Your program is to write to standard output. Print exactly one line. The line should contain the minimum size of $P'$ that makes a double rainbow. If there is no such $P'$, print $0$.