P14740 [ICPC 2021 Seoul R] Logistical Warehouse 2

**KOPANG** 是韩国最大的在线零售商之一，并首次推出了所谓的“清晨配送”服务。为了应对不断增长的需求，**KOPANG** 计划建设新的物流仓库。物流仓库的位置必须与客户保持在一定距离之内，以确保 **KOPANG** 向客户承诺的配送时间。 物流网络被建模为一棵连通的树 $T$。$T$ 的每个节点代表一个区域，例如韩国的城市或省份；$T$ 的每条边代表连接两个区域的运输道路。**KOPANG** 希望选择一个或多个 $T$ 的节点作为物流仓库，以满足 **距离限制**。在选择之前，**KOPANG** 首先通过充分的研究确定了一个距离参数 $K$。现在，**KOPANG** 希望选择最少数量的节点来满足距离限制，即 $T$ 中每个节点到其最近被选节点（仓库）的距离不超过 $K$。两个节点 $u$ 和 $v$ 之间的距离定义为连接 $u$ 和 $v$ 的（唯一）路径上的边数。注意，如果 $u = v$，距离定义为 $0$。 例如，下图 G.1 展示了一棵有九个节点和八条边的树 $T$。对于 $K = 1$，如果将三个仓库设在节点 2、5 和 8（如图 G.1 (a) 中红色圆圈标记所示），那么 $T$ 中每个节点到最近仓库的距离都至多为 $1$。两个仓库不足以满足距离限制，因此三个仓库是最小数。对于 $K = 2$，仍然需要三个仓库；$K = 1$ 时在节点 2、5 和 8 设立的仓库对 $K = 2$ 也适用。当然，最小数量仓库的位置并不唯一；如图 G.1 (b) 所示，在节点 4、7 和 1 设立三个仓库也能满足 $K = 2$ 时的距离限制。 给定一棵连通的树 $T$ 和一个正整数 $K$，请编写一个程序来选择最少数量的节点（仓库）以满足距离限制，即 $T$ 中每个节点到其最近仓库的距离不超过 $K$。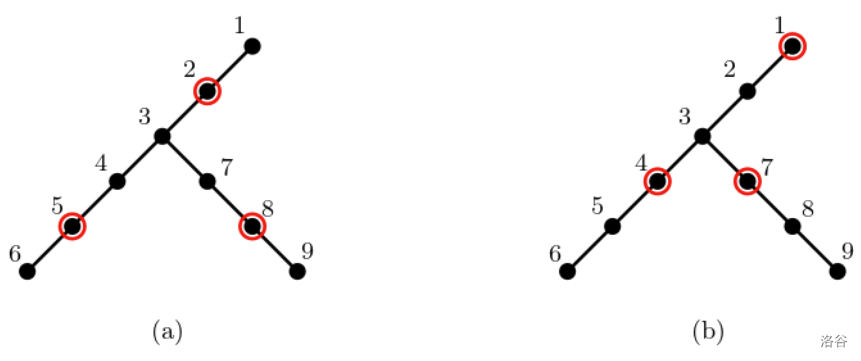 :::align{center}  图 G.1 用红色圆圈标记的节点是被选为仓库的节点。 :::

你的程序需要从标准输入读取数据。输入的第一行包含两个整数 $n$ 和 $K$ ($1 \le K \le n \le 10^5$)，其中 $n$ 是连通树中的节点数，树中每个节点到其最近被选节点的最大距离不超过 $K$。接下来的 $n-1$ 行给出边的信息；第 $i$ 行包含两个正整数，表示第 $i$ 条边两个端节点的索引。节点的索引从 $1$ 到 $n$。

你的程序需要向标准输出写入结果。输出恰好一行，包含为满足给定树和距离参数 $K$ 的距离限制而选择的物流仓库的最小数量。

翻译由 DeepSeek V3 完成