P14744 [ICPC 2021 Seoul R] Stock Price Prediction

金先生是一位股票市场分析师。最近，他在查看几家公司的股票图表时发现了一些有趣的现象。大多数连续上涨四天的股票在第五天会下跌。而且，第五天下跌时的股价，通常位于这四天上涨期间第二天和第三天的股价之间。例如，A 公司的股价连续四天为 $500$ 韩元、$560$ 韩元、$600$ 韩元和 $680$ 韩元，而 A 公司第五天的股价是 $580$ 韩元。同样，B 公司的股价连续四天为 $1,000$ 韩元、$1,200$ 韩元、$1,400$ 韩元和 $1,700$ 韩元，而 B 公司第五天的股价是 $1,350$ 韩元。 金先生认为，如果能在之前的股价序列中找到与最近几天价格变动模式相匹配的部分，他将能够相当准确地预测下一天的股价。他还认为，股价序列中的相对排名比实际价格更重要，因为如果两个股价序列的相对排名相同，它们在图表上的形态看起来就会相似。在上面的例子中，A 公司连续五天的股价序列 $500$ 韩元、$560$ 韩元、$600$ 韩元、$680$ 韩元、$580$ 韩元可以表示为 $(1,2,4,5,3)$，因为 $500$ 是五个数中最小的，$560$ 是第二小的，$600$ 是第四小的，依此类推。此外，B 公司连续五天的股价序列 $1,000$ 韩元、$1,200$ 韩元、$1,400$ 韩元、$1,700$ 韩元、$1,350$ 韩元，由于同样的原因，也可以表示为 $(1,2,4,5,3)$。它们的相对排名相同，并且它们连续五天的图表看起来非常相似，如图 K.1 所示。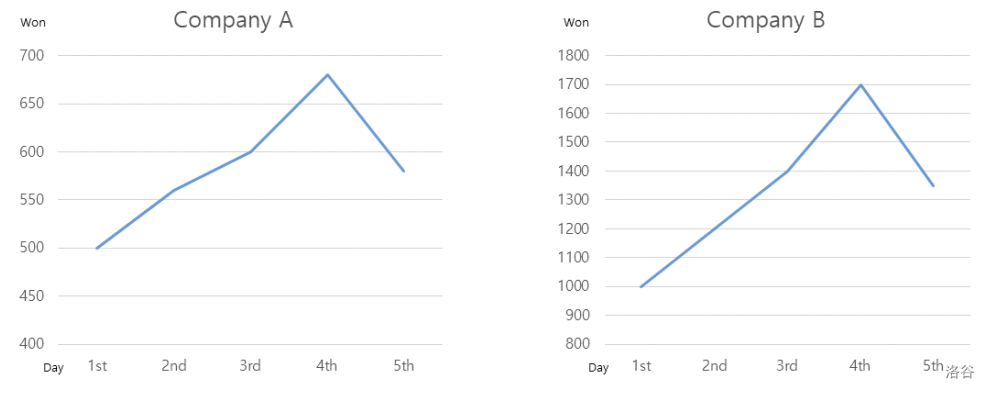 :::align{center}  图 K.1 A 公司和 B 公司连续五天的图表 ::: 金先生决定，如果两个序列相同位置的相对排名都相同，则认为这两个序列匹配。金先生正式定义了相同长度（整数个数）的两个序列的 **R 匹配** 如下：两个长度相同的整数序列 $x = (x_1, ..., x_m)$ 和 $y = (y_1, ..., y_m)$ 是 **R 匹配** 当且仅当对于每个 $i$ ($1 \le i \le m$)，$x_i$ 在 $x$ 中的排名与 $y_i$ 在 $y$ 中的排名相同。接着，他将 **R 模式匹配问题** 定义如下：给定两个整数序列 $x$（长度为 $m$）和 $y$（长度为 $n$，$m \le n$），找出 $y$ 中所有满足 $x$ 与 $(y_i, ..., y_{i+m-1})$ 是 **R 匹配** 的位置 $i$。例如，当 $x = (33,40,22,40,41,28)$，$y = (10,20,16,27,32,12,32,33,20,25,15,25,31,17)$ 时，$x$ 与 $(y_4, ..., y_9)$ 是 **R 匹配**，并且 $x$ 与 $(y_9, ..., y_{14})$ 也是 **R 匹配**。 给定两个整数序列 $x$（长度为 $m$）和 $y$（长度为 $n$，$m \leq n$），请编写一个程序来解决 $x$ 和 $y$ 的 R 模式匹配问题。

你的程序需要从标准输入读取数据。输入的第一行包含两个整数 $m$ 和 $n$ ($1 \leq m \leq 10,000$, $1 \leq n \leq 1,000,000$, $m \leq n$)，其中 $m$ 是 $x$ 的长度，$n$ 是 $y$ 的长度。第二行依次给出 $x$ 中的 $m$ 个整数。第三行依次给出 $y$ 中的 $n$ 个整数。$x$ 和 $y$ 中的每个整数均在 $1$ 到 $10^9$ 的范围内。

你的程序需要向标准输出写入结果。输出恰好一行。该行应包含 $y$ 中所有满足 $x$ 与 $(y_i, \dots, y_{i+m-1})$ 是 R 匹配的位置 $i$。每个位置必须按递增顺序出现。如果没有这样的位置，则输出 $0$。

翻译由 DeepSeek V3 完成