P14767 [ICPC 2024 Seoul R] Colorful Quadrants

You are given an $ n \times n $ grid, and some of the grid points are colored by one of the $ k $ colors. The color of a point is represented by an integer from 0 to $ k $, where 0 represents the uncolored case. Note that multiple points may be colored the same. The rows and columns of the grid are denoted by integers from 1 to $ n $, and a point located at row $ i $ and column $ j $ is denoted by $ (i,j) $. For an uncolored point $ (i,j) $ that satisfies $ 1 < i < n $ and $ 1 < j < n $, we define four sub-grids by removing row $ i $ and column $ j $ from the grid. Each of the four sub-grids is called NW (northwest), NE (northeast), SW (southwest), and SE (southeast) based on the position relative to $ (i,j) $. We say that $ (i,j) $ has **colorful quadrants** if, when selecting one point from each of the four sub-grids, the chosen four points are all of different colors. See Figure C.1(a) as a $ 5 \times 5 $ grid example. The point $ (2,3) $ has colorful quadrants because NW has color 1, NE has color 4, SW has color 3, and SE has color 2, as shown in Figure C.1(b). However, the point $ (4,3) $ does not have colorful quadrants because both SW and SE have color 2 only, as shown in Figure C.1(c). 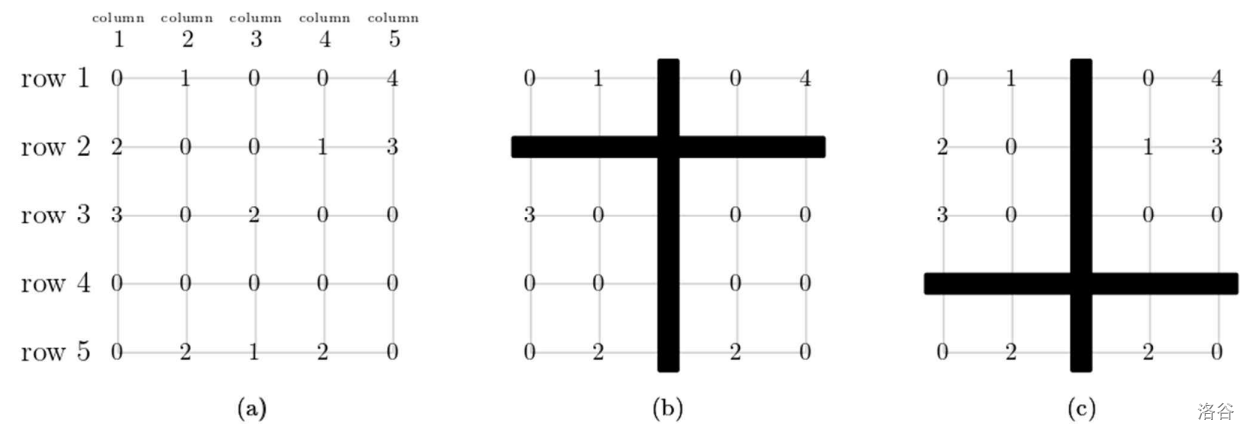:::align{center}  Figure C.1 ::: Given an $ n \times n $ grid containing at least four grid points colored in different colors, write a program to count the number of uncolored points that have colorful quadrants.

Your program is to read from standard input. The input starts with a line containing two integers, $ n $ and $ k $ ($ 3 \leq n \leq 2,000 $, $ 4 \leq k \leq 1,000 $), where $ n $ is the number of rows and columns of the grid and $ k $ is the number of colors. In the following $ n $ lines, the $ i $-th line contains $ n $ integers that represent the colors of the points $ (i,j) $ for $ 1 \leq j \leq n $. The integer $ c $ that represents the color of a point is in range $ 0 \leq c \leq k $.

Your program is to write to standard output. Print exactly one line. The line should contain the number of uncolored points that have colorful quadrants.