P14767 [ICPC 2024 Seoul R] Colorful Quadrants

给定一个 $n \times n$ 的网格，其中部分网格点被 $k$ 种颜色之一着色。点的颜色用一个 $0$ 到 $k$ 的整数表示，其中 $0$ 表示未着色的情况。注意，多个点可能被涂成相同的颜色。网格的行和列用 $1$ 到 $n$ 的整数表示，位于第 $i$ 行、第 $j$ 列的点记作 $(i,j)$。对于一个满足 $1 < i < n$ 且 $1 < j < n$ 的未着色点 $(i,j)$，我们通过从网格中移除第 $i$ 行和第 $j$ 列，定义四个子网格。这四个子网格根据其相对于 $(i,j)$ 的位置，分别称为 **NW**（西北）、**NE**（东北）、**SW**（西南）和 **SE**（东南）。如果从这四个子网格中各选一个点，所选的四个点颜色各不相同，则称 $(i,j)$ 具有 **多彩象限**。 参见图 C.1(a) 作为一个 $5 \times 5$ 网格的例子。点 $(2,3)$ 具有多彩象限，因为 NW 子网格有颜色 1，NE 有颜色 4，SW 有颜色 3，SE 有颜色 2，如图 C.1(b) 所示。然而，点 $(4,3)$ 不具有多彩象限，因为 SW 和 SE 子网格都只有颜色 2，如图 C.1(c) 所示。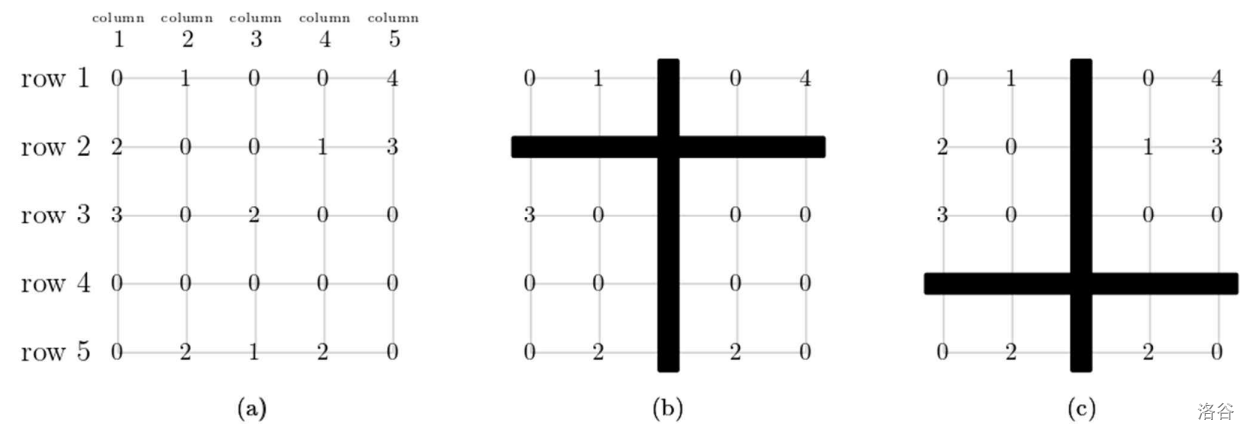 :::align{center}  图 C.1 ::: 给定一个 $n \times n$ 的网格，其中至少包含四个被涂上不同颜色的网格点，请编写一个程序，统计具有多彩象限的未着色点的数量。

你的程序需要从标准输入读取数据。输入的第一行包含两个整数 $n$ 和 $k$ ($3 \leq n \leq 2,000$, $4 \leq k \leq 1,000$)，其中 $n$ 是网格的行数和列数，$k$ 是颜色的数量。接下来的 $n$ 行中，第 $i$ 行包含 $n$ 个整数，表示点 $(i,j)$ ($1 \leq j \leq n$) 的颜色。表示点颜色的整数 $c$ 在 $0 \leq c \leq k$ 的范围内。

你的程序需要向标准输出写入结果。输出恰好一行。该行应包含具有多彩象限的未着色点的数量。

翻译由 DeepSeek V3 完成