P14770 [ICPC 2024 Seoul R] Pair Sorting

There are $ n $ bins arranged in a row and $ 2n $ balls on the ground. The balls are numbered from 1 to $ n $ and there are exactly two balls numbered $ i $, for each $ i $, $ 1 \leq i \leq n $. Also, for $ 1 \leq i \leq n $, the $ i $-th bin is denoted by $ B_i $ and each bin $ B_i $ can contain at most two balls. Initially, the bin $ B_i $ contains both of ball $ n+1-i $'s, for $ 1 \leq i \leq n $. See the Figure F.1 below for the initial configuration of bins. 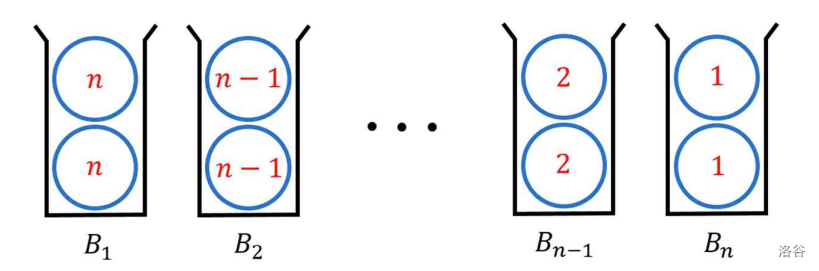:::align{center}  Figure F.1. The initial configuration of bins ::: You can swap two balls only from adjacent bins, which implies one swap operation. Note the bin is not a stack and for adjacent bins $ B_i $ and $ B_{i+1} $, you can swap the one of two balls in $ B_i $ and the one in $ B_{i+1} $. See the Figure F.2 below. The figure represents two swap operations. 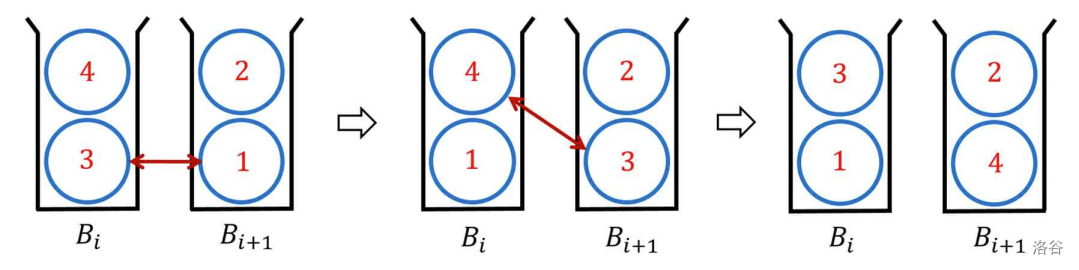:::align{center}  Figure F.2. The swap operations between adjacent bins ::: Through these swap operations, you should sort the balls. As a result of the sorting, the bin $ B_i $ must contain the both of ball $ i $'s, for $ 1 \leq i \leq n $. In particular, the total number of swap operations should be no more than $ \text{Bound} $, when $ \text{Bound} $ is given as a function of $ n $, especially, $ \text{Bound} = 0.7n^2 $. Given $ n $ bins and $ 2n $ balls, write a program to find a sorting method of balls such that the total number of swap operations is no more than $ \text{Bound} = 0.7n^2 $.

Your program is to read from standard input. The input consists of exactly one line. The line contains an integer $ n $ ($ 3 \leq n \leq 100 $), representing that there are $ n $ bins and $ 2n $ balls.

Your program is to write to standard output. Let $ S $ be the total number of swap operations in your sorting method for the input. Print exactly $ S+1 $ lines. The first line contains $ S $. Each of the following $ S $ lines contains three integers $ j, a, $ and $ b $, representing one swap operation between the ball $ a $ in the bin $ B_j $ and the ball $ b $ in $ B_{j+1} $, where $ 1 \leq j \leq n-1 $ and $ 1 \leq a, b \leq n $. The swap operations in your sorting method should be printed in order, one per line. The number $ S $ must satisfy that $ S \leq 0.7n^2 $.