P14792 [NERC 2025] Knit the Grid

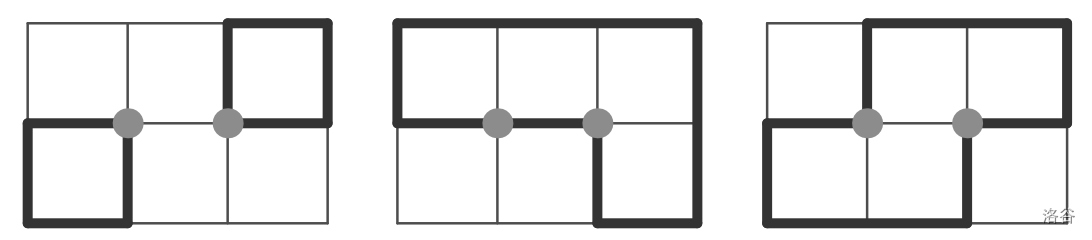
一位巫毒女士曾编织了一幅魔法挂毯。起初，她拿了一块空白画布，可以表示为一个 $r \times c$ 的网格，有 $r$ 行和 $c$ 列，因此有 $(r + 1) \times (c + 1)$ 个网格点。然后她进行了若干次如下操作：她沿着网格线在画布上编织一个环，该环中每个网格点最多被经过一次。此外，任意两个环不共享任何网格点。 最终，对于不在画布边界上的 $(r - 1) \times (c - 1)$ 个内部网格点，每个点恰好被一个环经过。以下是 $r=2$、$c=3$ 时的一些环排列示例，内部网格点已高亮显示： :::align{center}  ::: 然后她将画布留在地板上过夜。夜间，$r \times c$ 只绿色青蛙跳上了画布，每只青蛙坐在一个单元格里。但这只是巫毒女士麻烦的开始！因为随后，老巫婆来到画布前，一个接一个地撕掉了画布上所有编织的线条。每次她撕掉两个相邻网格点之间的编织线段时，与该线段相邻的单元格中的青蛙会受到惊吓（根据线段是否在边界上，会有一只或两只青蛙受到惊吓）。当青蛙受到惊吓时，它会立即改变颜色：如果青蛙是绿色的，它会变成棕色；如果是棕色的，它会变回绿色。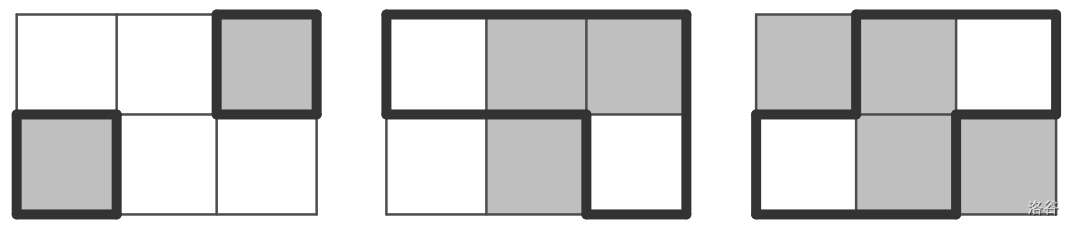 如果环的排列如上图所示，那么颜色将如下所示（灰色单元格代表绿色青蛙，白色单元格代表棕色青蛙）： :::align{center}  ::: 当巫毒女士回到她的画布前时，她只看到画布上有两种颜色的青蛙，但编织的环都不见了。根据给定的青蛙颜色排列，判断它是否可能是由上述过程产生的，如果是，请帮助巫毒女士恢复一种可能的环排列。

每个测试包含多个测试用例。第一行包含测试用例的数量 $t$ ($1 \le t \le 10^4$)。接下来是测试用例的描述。 每个测试用例的第一行包含两个整数 $r$ 和 $c$，表示网格的尺寸 ($2 \le r, c \le 10^3$)。 接下来的 $r$ 行，每行包含一个由 $c$ 个字符组成的字符串，字符为 $\texttt{G}$ 或 $\texttt{B}$，分别表示绿色和棕色青蛙。 保证所有测试用例的 $r \times c$ 之和不超过 $2 \times 10^6$。

对于每个测试用例，如果给定的青蛙颜色可能是由上述过程产生的，则在第一行输出 $\texttt{YES}$，否则输出 $\texttt{NO}$。 如果答案是 $\texttt{YES}$，则额外输出 $2r+1$ 行二进制字符串（由 $\texttt{0}$ 和 $\texttt{1}$ 字符组成）。前 $r+1$ 行每行长度为 $c$，表示水平网格线段；接下来的 $r$ 行每行长度为 $c+1$，表示垂直网格线段，具体解释如下。 在前 $r+1$ 行中，第 $i$ 行的第 $j$ 个字符为 $\texttt{1}$，表示从左数第 $j$ 条、从上数第 $i$ 条的水平网格线段应有一条编织线经过，否则为 $\texttt{0}$。 在接下来的 $r$ 行中，第 $i$ 行的第 $j$ 个字符为 $\texttt{1}$，表示从左数第 $j$ 条、从上数第 $i$ 条的垂直网格线段应有一条编织线经过，否则为 $\texttt{0}$。

第一个测试用例是题目描述中的第一个环排列示例。 在第二个样例测试用例中，样例中展示的输出如下图所示的第一张图。第二张图中的环排列也是正确的，而第三张图中的排列不正确，因为有些网格点被多个环共享。保持网格为空也是不正确的，因为没有环经过内部网格点。 :::align{center}  :::