P1479 Stories in the Dormitory: Gomoku

There are lots and lots of fun things in the dormitory! Today 7890653 saw Gomoku, which had unknowingly become popular. In the dorm, they took a notebook, drew some squares, and a board was ready. When 7890653 looked at the board, an idea came to mind... On a $5 \times 5$ board, place $n$ stones, where $5 \le n \le 25$; the $n$ stones can be placed anywhere on the board, but they cannot overlap. Thus, there may be five stones forming a row, a column, or lying on the same diagonal. Different placements may produce different numbers of five-in-a-row lines. Your task: given $n$, find all possible counts $k$ of five-in-a-row lines that can appear over different placements (counting full lines among the 5 rows, 5 columns, and 2 diagonals). 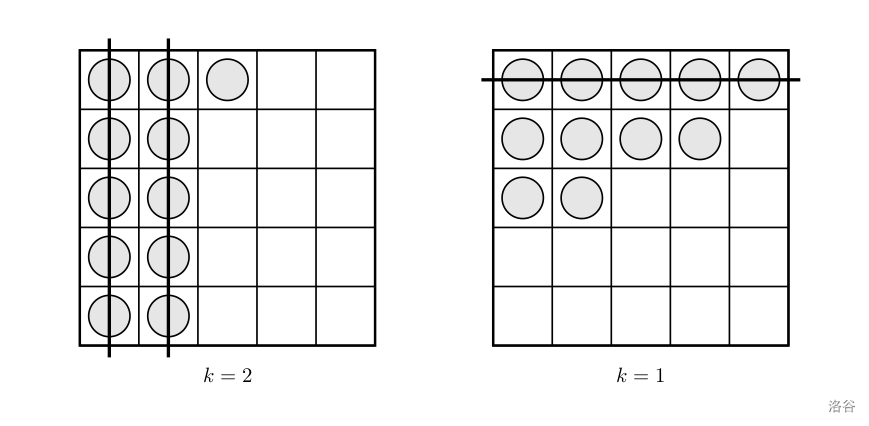For example, when $n = 11$, we have:  Only these two nonnegative $k$ values occur (note that $k$ values are not repeated). You should output the sum of these distinct $k$ values. That is, $1 + 2 = 3$.

The input contains one line with a single integer $n$, as described. Guaranteed $1 \le n \le 25$.

Output the sum of all possible $k$ values. It is easy to see that $k \le 12$.

Translated by ChatGPT 5