P14814 [ICPC 2023 Yokohama R] Yokohama Phenomena

你听说过横滨现象吗？这种现象发生在三位程序员围坐在一张桌子旁，共同握着一支笔悬在一块木板上方时。木板上画着一个方格网格，每个方格标有一个字母。尽管没有任何参与者有意移动这支笔，但它的笔尖仿佛有自己的意志，会落到其中一个标有 Y 的方格上，然后开始在木板上移动。经过的方格按顺序标有 O、K、O、H、A 和 M，然后笔尖停在标有 A 的方格上。 让我们将笔尖沿着这样的轨迹经过的方格序列称为一个 **YOKOHAMA 轨迹**。YOKOHAMA 轨迹定义如下： - 它是给定方格网格中由八个方格组成的序列。 - 该序列中除第一个方格外的每个方格，都与其序列中的直接前一个方格共享一条边（即边相邻）。 - 序列中八个方格所标的字母按顺序为 Y、O、K、O、H、A、M 和 A。 注意，同一个方格可能在序列中出现多次。 图 A.1 (a) 展示了对应于样例输入 1 的木板的示意图。图 A.1 (b) 和 (c) 显示了两个 YOKOHAMA 轨迹上的路径。两个轨迹都起始于最上一行的最左边方格。在图 A.1 (c) 所示的轨迹中，标有 O 的同一个方格出现了两次。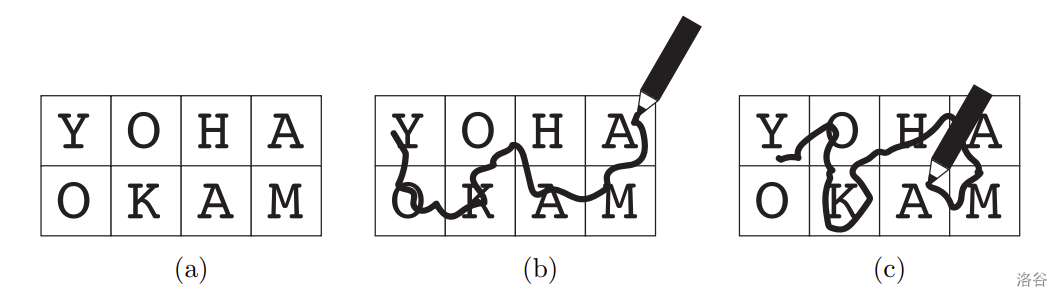 :::align{center}  图 A.1. 一个木板及两个 YOKOHAMA 轨迹上的路径 ::: 你被给予一个方格网格，每个方格标有六个字母 A、H、K、M、O 或 Y 中的一个。你的任务是计算在该网格上有多少种不同的 YOKOHAMA 轨迹。

输入包含一个单独的测试用例，格式如下。 $$ \begin{aligned} &n\ m \\ &x_{1,1}\ \cdots\ x_{1,m} \\ &\vdots \\ &x_{n,1}\ \cdots\ x_{n,m} \end{aligned} $$ 前两个整数 $n$ 和 $m$ ($1 \le n \le 10$, $1 \le m \le 10$) 描述了网格的大小。网格中的方格排列成一个 $n \times m$ 的矩阵。接下来的 $n$ 行描述了方格中所标的字母。网格中第 $i$ 行第 $j$ 列的方格 ($1 \le i \le n$, $1 \le j \le m$) 标有字母 $x_{i,j}$。每个 $x_{i,j}$ 是六个字母 A、H、K、M、O 或 Y 中的一个。

输出一行，包含不同的 YOKOHAMA 轨迹的数量。

翻译由 DeepSeek V3 完成