P14819 [ICPC 2023 Yokohama R] Color Inversion on a Huge Chessboard

你被给予一个按棋盘状排列的方格集合，有 $n$ 行和 $n$ 列。行从上到下编号为 $1$ 到 $n$，列从左到右也编号为 $1$ 到 $n$。 初始时，方格像国际象棋棋盘一样着色：如果 $i + j$ 为奇数，则位于第 $i$ 行第 $j$ 列的方格为黑色；如果为偶数，则为白色。 随后依次进行颜色反转操作，每次操作是以下两种之一： **反转某行的颜色**：给定一个行号，反转指定行中所有方格的颜色。该行中的白色方格变为黑色，黑色方格变为白色。 **反转某列的颜色**：给定一个列号，反转指定列中所有方格的颜色。该列中的白色方格变为黑色，黑色方格变为白色。 需要在每次操作后统计不同的 **区域** 数量。这里，区域是指由相同颜色、直接或间接相连的方格组成的集合。当两个方格共享一条边时，称它们直接相连。

输入由单个测试用例组成，格式如下。 $$\begin{aligned} &n\ q \\ &operation_1 \\ &\vdots \\ &operation_q \end{aligned}$$ 整数 $n$ 是行数和列数 ($1 \leq n \leq 5 \times 10^5$)。整数 $q$ 是操作的数量 ($1 \leq q \leq 5 \times 10^5$)。接下来的 $q$ 行按顺序表示要执行的操作。每行是以下两种形式之一： - **ROW $i$**：表示对第 $i$ 行 ($1 \leq i \leq n$) 执行“反转某行的颜色”操作。 - **COLUMN $j$**：表示对第 $j$ 列 ($1 \leq j \leq n$) 执行“反转某列的颜色”操作。

输出 $q$ 行。第 $k$ 行应包含一个整数，表示第 $k$ 次操作后区域的数量。

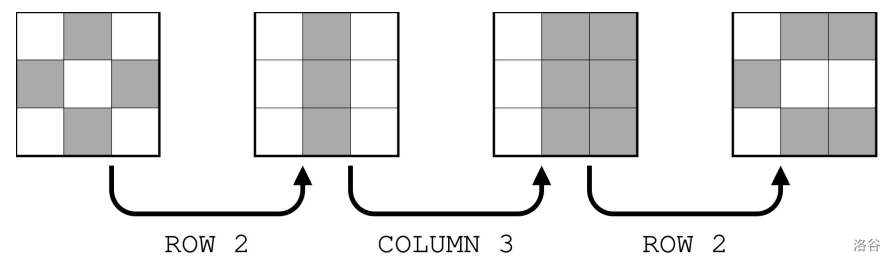
:::align{center}  图 F.1. 样例输入 1 的示意图 :::