P14823 [ICPC 2023 Yokohama R] Do It Yourself?

You are the head of a group of $n$ employees including you in a company. Each employee has an employee ID, which is an integer 1 through $n$, where your ID is 1. Employees are often called by their IDs for short: $\#1$, $\#2$, and so on. Every employee other than you has a unique *immediate boss*, whose ID is smaller than his/hers. A *boss* of an employee is transitively defined as follows. - If an employee $\#i$ is the immediate boss of an employee $\#j$, then $\#i$ is a boss of $\#j$. - If $\#i$ is a boss of $\#j$ and $\#j$ is a boss of $\#k$, then $\#i$ is a boss of $\#k$. Every employee including you is initially assigned exactly one task. That task can be done by him/herself or by any one of his/her bosses. Each employee can do an arbitrary number of tasks, but doing many tasks makes the employee too tired. Formally, each employee $\#i$ has an individual fatigability constant $f_i$, and if $\#i$ does $m$ tasks in total, then the *fatigue level* of $\#i$ will become $f_i \times m^2$. Your mission is to minimize the sum of fatigue levels of all the $n$ employees.

The input consists of a single test case in the following format. $$ \begin{aligned} & n \\ & b_2 \ b_3 \ \cdots \ b_n \\ & f_1 \ f_2 \ \cdots \ f_n \\ \end{aligned} $$ The integer $n$ in the first line is the number of employees, where $2 \leq n \leq 5 \times 10^5$. The second line has $n-1$ integers $b_i$ ($2 \leq i \leq n$), each of which represents the immediate boss of the employee $\#i$, where $1 \leq b_i < i$. The third line has $n$ integers $f_i$ ($1 \leq i \leq n$), each of which is the fatigability constant of the employee $\#i$, where $1 \leq f_i \leq 10^{12}$.

Output the minimum possible sum of fatigue levels of all the $n$ employees.

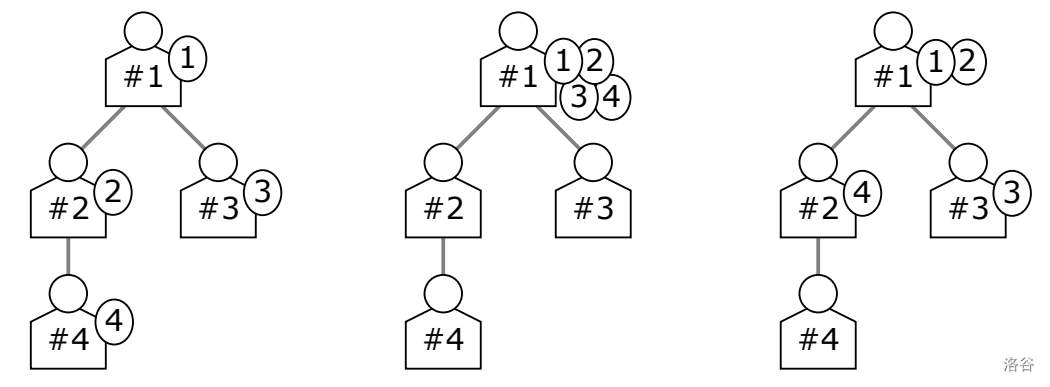
:::align{center}  Figure J.1. Illustration of the three samples (from left to right) ::: The situations and solutions of the three samples are illustrated in Figure J.1. For Sample Input 1, the unique optimal way is that each employee does his/her task by him/herself. That is, you should just say "Do it yourself!" to everyone. For Sample Input 2, the unique optimal way is that the employee $\#1$ does all the tasks. That is, you should just say "Leave it to me!" to everyone. For Sample Input 3, one of the optimal ways is the following. - $\#1$ does the tasks of $\#1$ and $\#2$, and then the fatigue level of $\#1$ will be $1 \times 2^2 = 4$. - $\#2$ does the task of $\#4$, and then the fatigue level of $\#2$ will be $2 \times 1^2 = 2$. - $\#3$ does the initially assigned task, and then the fatigue level of $\#3$ will be $4 \times 1^2 = 4$. - $\#4$ does nothing, and then the fatigue level of $\#4$ will be $8 \times 0^2 = 0$. Thus, the sum of the fatigue levels is $4 + 2 + 4 + 0 = 10$. There is another optimal way, in which the employees $\#1$, $\#2$, and $\#3$ do their initially assigned tasks by themselves and $\#1$ does the task of $\#4$ in addition.