P14823 [ICPC 2023 Yokohama R] Do It Yourself?
题目描述
你是一家公司里包括你在内的 $n$ 名员工的负责人。每名员工有一个员工 ID,是一个 $1$ 到 $n$ 的整数,你的 ID 是 $1$。员工通常简称为 $\#1$、$\#2$ 等。除你之外的每名员工都有一个唯一的 **直属上司**,其 ID 小于他/她的 ID。一名员工的 **上司** 通过传递性定义如下:
- 如果员工 $\#i$ 是员工 $\#j$ 的直属上司,那么 $\#i$ 是 $\#j$ 的上司。
- 如果 $\#i$ 是 $\#j$ 的上司,且 $\#j$ 是 $\#k$ 的上司,那么 $\#i$ 是 $\#k$ 的上司。
包括你在内的每名员工最初恰好被分配一项任务。该任务可以由他/她自己完成,也可以由他/她的任意一位上司完成。每名员工可以完成任意数量的任务,但完成过多任务会使员工过度疲劳。形式化地说,每名员工 $\#i$ 有一个个体疲劳度常数 $f_i$,如果 $\#i$ 总共完成 $m$ 项任务,那么 $\#i$ 的 **疲劳水平** 将变为 $f_i \times m^2$。
你的使命是最小化所有 $n$ 名员工的疲劳水平之和。
输入格式
输入由单个测试用例组成,格式如下。
$$
\begin{aligned}
& n \\
& b_2 \ b_3 \ \cdots \ b_n \\
& f_1 \ f_2 \ \cdots \ f_n \\
\end{aligned}
$$
第一行的整数 $n$ 是员工数量,其中 $2 \leq n \leq 5 \times 10^5$。第二行有 $n-1$ 个整数 $b_i$ ($2 \leq i \leq n$),每个代表员工 $\#i$ 的直属上司,其中 $1 \leq b_i < i$。第三行有 $n$ 个整数 $f_i$ ($1 \leq i \leq n$),每个是员工 $\#i$ 的疲劳度常数,其中 $1 \leq f_i \leq 10^{12}$。
输出格式
输出所有 $n$ 名员工的疲劳水平之和的最小可能值。
说明/提示
:::align{center}
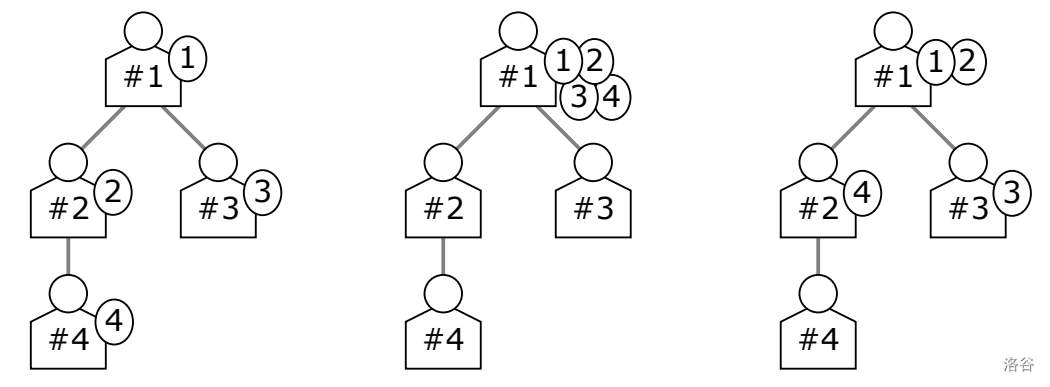
图 J.1. 三个样例的示意图(从左到右)
:::
三个样例的情况和解决方案如图 J.1 所示。
对于样例输入 1,唯一的最优方式是每名员工自己完成自己的任务。也就是说,你只需对每个人说“你自己做吧!”。
对于样例输入 2,唯一的最优方式是员工 $\#1$ 完成所有任务。也就是说,你只需对每个人说“交给我吧!”。
对于样例输入 3,一种最优方式如下:
- $\#1$ 完成 $\#1$ 和 $\#2$ 的任务,那么 $\#1$ 的疲劳水平为 $1 \times 2^2 = 4$。
- $\#2$ 完成 $\#4$ 的任务,那么 $\#2$ 的疲劳水平为 $2 \times 1^2 = 2$。
- $\#3$ 完成最初分配的任务,那么 $\#3$ 的疲劳水平为 $4 \times 1^2 = 4$。
- $\#4$ 不做事,那么 $\#4$ 的疲劳水平为 $8 \times 0^2 = 0$。
因此,疲劳水平之和为 $4 + 2 + 4 + 0 = 10$。还存在另一种最优方式,即员工 $\#1$、$\#2$ 和 $\#3$ 自己完成最初分配的任务,并且 $\#1$ 额外完成 $\#4$ 的任务。
翻译由 DeepSeek V3 完成