P14845 [ICPC 2022 Yokohama R] Move One Coin

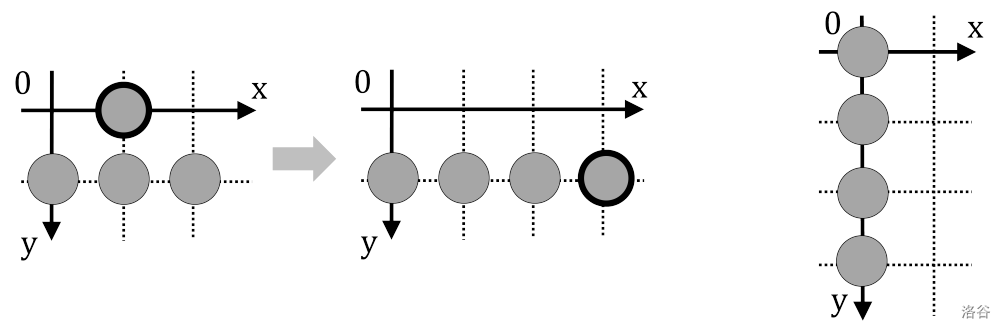
一些硬币被放置在一个二维平面的网格点上。没有两个硬币堆叠在同一个点上。我们将这种硬币的放置方式称为 **源模式**。同样数量硬币的另一种放置方式，称为 **目标模式**，也已给出。 源模式与目标模式不匹配，但通过将源模式中的恰好一枚硬币移动到一个空的网格点上，得到的新模式将与目标模式匹配。你的任务是找出这样的一次硬币移动。 这里，如果两种模式中，一种可以通过对平面进行若干次 90 度旋转和平移（但不能镜像）从另一种得到，则称它们 **匹配**。例如，在图 D.1 左侧的源模式中，通过将 $(1,0)$ 处的硬币移动到 $(3,1)$，我们得到右侧的模式，该模式与图 D.2 所示的目标模式匹配。 :::align{center}  图 D.1. 源模式及一次移动 图 D.2. 目标模式 :::

输入由单个测试用例组成，格式如下。 $$ \begin{aligned} &h\ w \\ &p_{0,0} \cdots p_{0,w-1} \\ &\vdots \\ &p_{h-1,0} \cdots p_{h-1,w-1} \\ &H\ W \\ &P_{0,0} \cdots P_{0,W-1} \\ &\vdots \\ &P_{H-1,0} \cdots P_{H-1,W-1} \\ \end{aligned} $$ 第一行包含两个整数 $h$ 和 $w$，均在 $1$ 到 $500$ 之间（含）。$h$ 是源模式描述的高度，$w$ 是宽度。接下来的 $h$ 行，每行由 $w$ 个字符组成，描述源模式。字符 $p_{y,x}$ 为 `'o'` 表示在 $(x,y)$ 处放置了一枚硬币，`'x'` 表示该处没有硬币。 接下来的行包含整数 $H$ 和 $W$ 以及字符 $P_{y,x}$，以相同方式描述目标模式。

如果答案是将位于 $(x_0, y_0)$ 的硬币移动到 $(x_1, y_1)$，则在第一行按顺序输出 $x_0$ 和 $y_0$，用一个空格分隔；在第二行按顺序输出 $x_1$ 和 $y_1$，用一个空格分隔。 保证至少存在一种满足要求的移动方案。当存在多个解决方案时，输出其中任意一个。 注意 $0 \leq x_0 < w$ 和 $0 \leq y_0 < h$ 始终成立，但 $x_1$ 和/或 $y_1$ 可能超出这些范围。