P14853 [ICPC 2021 Yokohama R] Loop of Chocolate

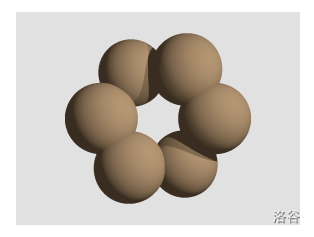
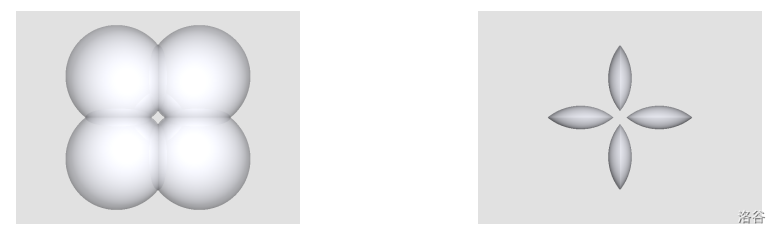
让我们制作一种形状别致的糖果——巧克力环。 :::align{center}  图 A.1. 由六个球体的并集形成的巧克力环 ::: 环的形状由若干个相同大小的球体的并集形成，其中每个球体恰好与另外两个球体相交。 :::align{center}  (a) 四个球体的并集 (b) (a) 中四个球体的四个交集 图 A.2. 由四个球体的并集形成的巧克力环 ::: 你的任务是编写一个程序，根据给定的球体大小和位置，计算这些球体并集的总体积，即填充该并集所形成的环所需的巧克力量。 [提示] 两个相同半径 $r$ 的球体，当它们的中心距离 $d$ 小于 $2r$ 时相交。已知相交部分的体积为 $$ \frac{2}{3}\pi(r - d/2)^2(2r + d/2). $$ 半径为 $r$ 的球体体积为 $4\pi r^3/3$。

输入由单个测试用例组成，格式如下。 $$ \begin{aligned} &n\ r \\ &x_1\ y_1\ z_1 \\ &\vdots \\ &x_n\ y_n\ z_n \end{aligned} $$ $n$ 和 $r$ 是整数。$n$ 是球体的数量 ($4 \leq n \leq 100$)。所有球体具有相同的半径 $r$ ($2 \leq r \leq 100$)。$(x_k, y_k, z_k)$ 表示第 $k$ 个球体 ($k = 1, \dots, n$) 中心的坐标。$x_k$、$y_k$、$z_k$ 均为介于 $-100$ 到 $100$ 之间（含）的整数。 对于 $1 \leq k < n$，第 $k$ 个和第 $k+1$ 个球体相交。第 $1$ 个和第 $n$ 个球体也相交。没有其他球体对相交。

在一行中输出球体并集的体积。输出的相对误差应在 $10^{-7}$ 以内。