P14856 [ICPC 2021 Yokohama R] Wireless Communication Network

我们正在一个山脉地区建立无线通信网络。通信站将设立在各个山顶上。这些山顶位于一条直线上，且海拔各不相同。 为了最小化成本，我们的通信网络应具有树形结构，即具有最少边数的连通图。网络的结构，也就是哪些站与哪些其他站通信，应事先确定。 我们按以下步骤构建通信网络： 1. 初始时，每个站自成一棵树，仅包含该站。 2. 在每一步，我们通过在不同树中的两个站之间建立一条链路来合并两棵相邻的树。当一棵树中的一个山顶与另一棵树中的一个山顶之间的所有山顶都属于这两棵树之一时，称这两棵树 **相邻**。要建立链路的站是这两棵树中海拔最高的山顶上的站；由于山顶的海拔各不相同，这些站是唯一确定的。 3. 重复步骤 2，直到所有站都直接或间接地连接起来。 图 D.1 展示了样例 1 的树形结构形成示例。 当一个站检测到紧急事件时，应广播警报消息给所有站。接收到消息后，每个站会将消息转发给所有与其有直接链路的站，除了消息来源的那个站。网络的直径，即从任意站发起消息传播所需的足够跳数，取决于上述步骤 2 中对两棵树的选择。 为了估计广播的最坏情况延迟，我们希望找出通过上述过程可能构建的网络的**最大直径**。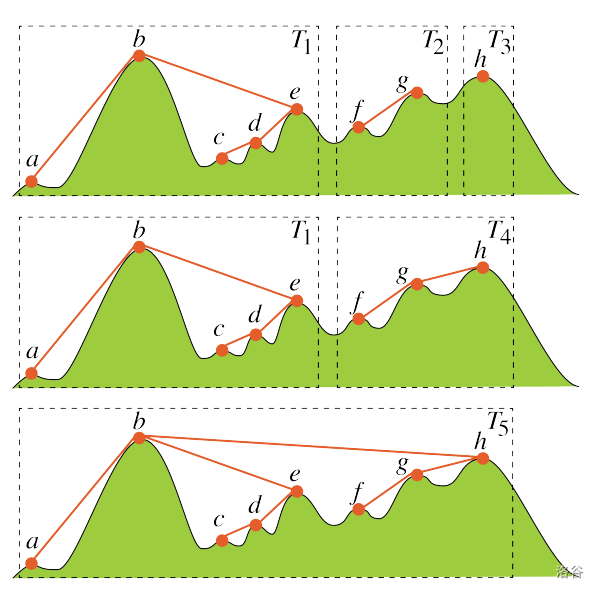 :::align{center}  图 D.1. 样例 1 的树形结构形成 ::: 经过特定一系列选择重复步骤 2 后得到的结果。此时有三棵树：$T_1$、$T_2$ 和 $T_3$。这里，站 $h$ 形成了仅包含该站的树 $T_3$。 通过在步骤 2 中连接站 $g$ 和 $h$ 得到的结果。树 $T_2$（最高山顶 $g$）和 $T_3$（最高山顶 $h$）是相邻的。 通过在下一步步骤 2 中连接站 $b$ 和 $h$ 合并两棵相邻的树后得到的结果。现在所有站形成了一棵树。

输入由单个测试用例组成，格式如下。 $$n$$ $$h_1$$ $$\vdots$$ $$h_n$$ 这里，$n$ 是通信站的数量 ($3 \leq n \leq 10^6$)，$h_i$ 是一个整数，表示第 $i$ 个站的海拔 ($1 \leq h_i \leq n$)。各站的海拔互不相同，即如果 $i \ne j$，则 $h_i \ne h_j$。

输出一行一个整数，表示树可能的最大直径。