P14861 [ICPC 2021 Yokohama R] "Even" Division

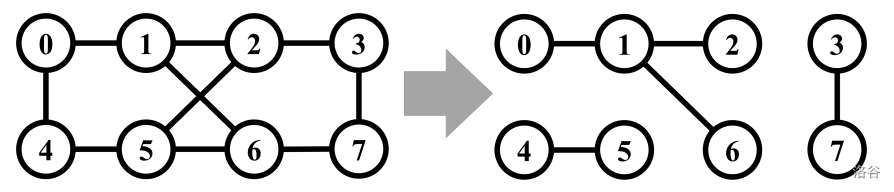
如果你谈论通常意义上的“偶数划分”，它意味着将事物等分。今天，你需要思考一些不同的东西。一个图需要被划分成子图，且每个子图的节点数为偶数，即二的倍数。 你被给予一个具有偶数个节点的无向连通图。给定的图将被划分为子图，使得所有子图都是连通的且具有偶数个节点，直到无法再进行这样的划分为止。图 1.1 展示了一个例子。原始的 8 个节点的图被划分为具有 4、2 和 2 个节点的子图。所有这些子图都具有偶数个节点。 :::align{center}  图 I.1. 一个划分示例（样例输入/输出 1） ::: 用数学术语来说，一个图的 **偶数划分** 是图节点子集 $V_1, \dots, V_k$ 的集合，满足以下条件： 1. $V_1 \cup \cdots \cup V_k$ 是输入图的所有节点的集合，且若 $i \neq j$，则 $V_i \cap V_j = \emptyset$。 2. 每个 $V_i$ 非空，且具有偶数个元素。 3. 每个 $V_i$ 导出一个连通的子图。换句话说，$V_i$ 中的任意节点都可以通过仅使用输入图中连接 $V_i$ 中两个节点的边相互可达。 4. 不存在进一步的划分。对于任意 $U_1 \cup U_2 = V_i$，用两个集合 $U_1$ 和 $U_2$ 替换 $V_i$ 得到的划分不满足条件 1、2 或 3 中的任意一条。 你的任务是找到给定图的一个 **偶数划分**。

输入由单个测试用例组成，格式如下。 $$ \begin{aligned} &n\ m \\ &x_1\ y_1 \\ &\vdots \\ &x_m\ y_m \end{aligned} $$ 第一行包含两个整数 $n$ 和 $m$。第一个整数 $n$ ($2 \leq n \leq 10^5$) 是一个偶数，表示要划分的图的节点数。第二个整数 $m$ ($n-1 \leq m \leq 10^5$) 是图的边数。 图的节点编号从 $0$ 到 $n-1$。 随后的 $m$ 行表示图的边。一行 $x_i\ y_i$ ($0 \leq x_i < y_i < n$) 意味着存在一条连接节点 $x_i$ 和 $y_i$ 的边。没有重复的边。保证输入图是连通的。

如果存在给定图的节点集到子集 $V_1, \dots, V_k$ 的 **偶数划分**，则在输出的第一行打印 $k$。接下来的 $k$ 行应描述子集 $V_1, \dots, V_k$。子集的顺序无关紧要。其中第 $i$ 行应以 $V_i$ 的大小开头，后跟 $V_i$ 中元素的节点编号，用一个空格分隔。节点编号的顺序也无关紧要。 如果有多个偶数划分，其中任意一个都可以接受。

在样例 2 中，原始图节点集的单元素集合本身已经是一个偶数划分。 翻译由 DeepSeek V3 完成