P14862 [ICPC 2021 Yokohama R] The Cross Covers Everything
题目描述
在 $x-y$ 平面上,一个十字形无限区域可以由两个不同的点指定,如下图所示。
:::align{center}
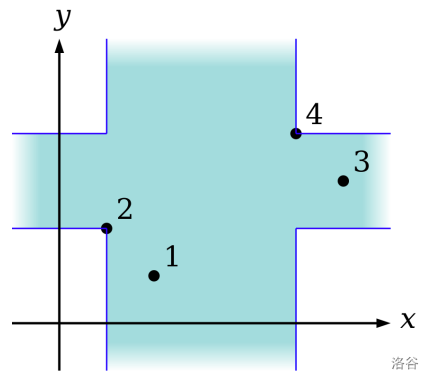
图 J.1. 由编号为 2 和 4 的两个点指定的十字区域
:::
给定平面上的一组点,你需要计算有多少对点形成的十字形区域覆盖了所有点。更精确地说,当给定坐标为 $(x_i, y_i)$ ($i = 1, \dots, n$) 的 $n$ 个点时,如果满足 $x_p \leq x \leq x_q$、$y_p \leq y \leq y_q$,或两者都成立,则有序对 $\langle p, q \rangle$ 称为覆盖点 $(x, y)$。你的任务是找出有多少对 $\langle p, q \rangle$ 覆盖了所有 $n$ 个点。给定的点中没有两个点具有相同的 $x$ 坐标或相同的 $y$ 坐标。
输入格式
输入由单个测试用例组成,格式如下。
$$
\begin{aligned}
&n \\
&x_1\ y_1 \\
&\vdots \\
&x_n\ y_n
\end{aligned}
$$
第一行包含一个整数 $n$ ($2 \leq n \leq 2 \times 10^5$),表示给定点的数量。接下来 $n$ 行中的第 $i$ 行包含两个整数 $x_i$ 和 $y_i$,表示第 $i$ 个点的坐标 ($1 \leq x_i \leq 10^6$, $1 \leq y_i \leq 10^6$)。你可以假设对于所有 $j \neq k$,有 $x_j \neq x_k$ 且 $y_j \neq y_k$。
输出格式
输出一行,表示满足条件的有序点对的数量。
说明/提示
图 J.1 描绘了由编号为 2 和 4 的两个点指定的十字区域,这两个点是样例输入 1 中的第二个和第四个点。这是覆盖所有点的十字之一。
### 修正
对于被计数的有序对 $\langle p, q \rangle$,需要满足条件 $x_p \leq x_q$ 和 $y_p \leq y_q$。这是在比赛期间宣布的。
翻译由 DeepSeek V3 完成