P14864 [ICPC 2020 Yokohama R] Three-Axis Views

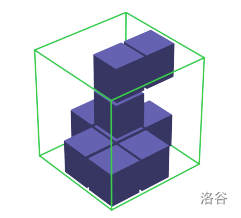
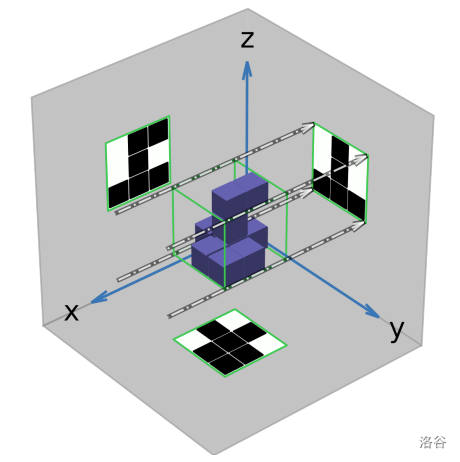
你的一位朋友是设计 **图像投影立方体 (ICPC)** 的艺术家。ICPC 是一个边长为整数的水晶立方体。通过精密的激光加工工艺，其部分区域被制成不透明的。每个不透明区域都是一个与整数坐标对齐的单位立方体。 图 A.1 描绘了如样例输入 1 中给出的一个 ICPC。图中，绿色线条对应水晶立方体的棱边。蓝色小立方体对应水晶内部的不透明立方区域。 :::align{center}  图 A.1. 样例输入 1 的 ICPC ::: ICPC 的乐趣在于欣赏其不透明区域在三个垂直于其表面的平行光源照射下产生的投影轮廓。图 A.2 描绘了该 ICPC 及其三个投影轮廓。 :::align{center}  图 A.2. 样例输入 1 的 ICPC 及其投影轮廓（点划线是垂直于左侧表面的平行光边缘） ::: 你的任务是编写一个程序，判断是否存在一个能产生给定投影轮廓的 ICPC。

输入由单个测试用例组成，格式如下。 $$n$$ $$s_1$$ $$\vdots$$ $$s_n$$ $$t_1$$ $$\vdots$$ $$t_n$$ $$u_1$$ $$\vdots$$ $$u_n$$ 这里，$n$ 是 ICPC 的尺寸，是一个介于 $1$ 到 $100$ 之间（含）的整数。 尺寸为 $n$ 的 ICPC 产生三个 $n \times n$ 的深色和浅色单元格投影轮廓。如果不透明单位立方体的阴影覆盖了单元格，则该单元格为深色，否则为浅色。从输入的第二行开始的 $3n$ 行，每行有 $n$ 个数字，表示 ICPC 的三个投影轮廓，其中 ‘0’ 表示浅色单元格，‘1’ 表示深色单元格。这 $3n$ 行中至少有一个数字是 ‘1’。 首先是 $yz$ 平面上的投影轮廓数据，其中第一行 $s_1$ 给出 $z$ 坐标值最大的轮廓单元格，按 $y$ 坐标顺序排列。接下来的行 $s_2, \dots, s_n$ 给出 $z$ 坐标值递减的单元格。 然后是 $zx$ 平面上的投影轮廓数据，其中第一行 $t_1$ 给出 $x$ 坐标值最大的轮廓单元格，按 $z$ 坐标顺序排列。接下来的行 $t_2, \dots, t_n$ 给出 $x$ 坐标值递减的单元格。 最后是 $xy$ 平面上的投影轮廓数据，其中第一行 $u_1$ 给出 $y$ 坐标值最大的轮廓单元格，按 $x$ 坐标顺序排列。接下来的行 $u_2, \dots, u_n$ 给出 $y$ 坐标值递减的单元格。 下图描绘了样例输入 1 中给出的 ICPC 的三个投影轮廓。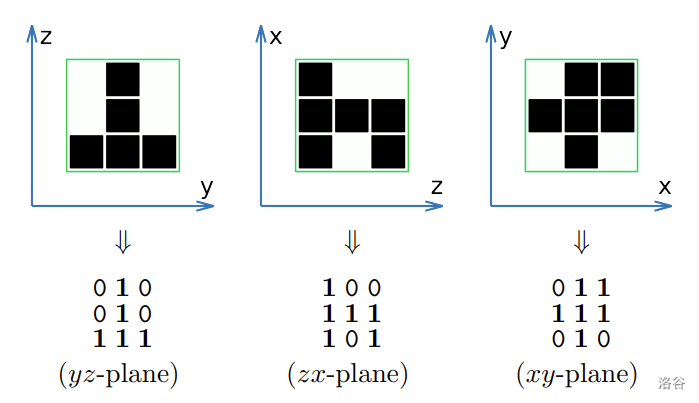 :::align{center}  图 A.3. 投影轮廓的 0-1 表示（样例输入 1） :::

如果可能制作出具有给定投影轮廓的 ICPC，则输出 “Yes”。否则输出 “No”。