P14868 [ICPC 2020 Yokohama R] Jewelry Size
题目描述
:::align{center}
:::
她想出了一种新的珠宝设计。该设计使用两个部分:一个空心的圆环和一个凸多边形部件。设计可以通过指定多边形的边长来定制,这些边长应该是单位长度的倍数,这样客户就可以在珠宝中嵌入纪念数字。请注意,可能存在许多具有指定边长的不同多边形。在这些多边形中,会选择那些有外接圆(即一个通过其所有顶点的圆)的多边形,以便多边形部件可以牢固地固定在圆环上。
:::align{center}
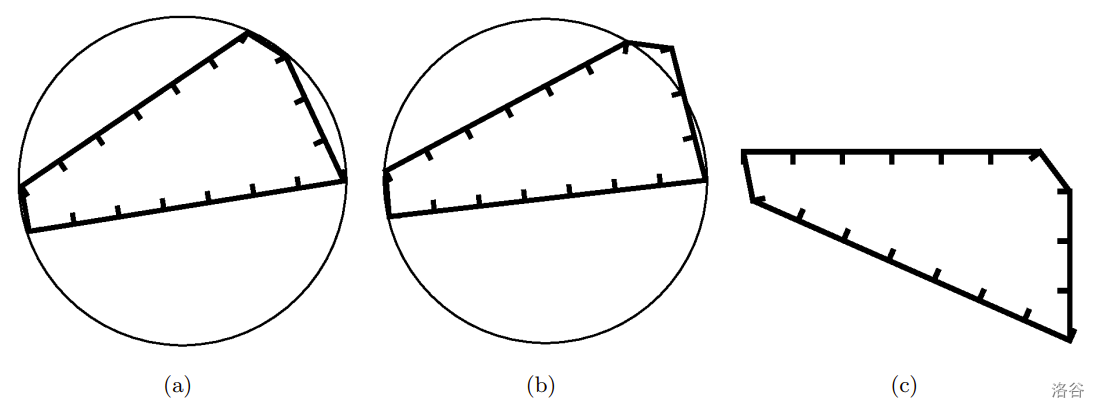
图 E.2. (a)一个有外接圆的五边形;(b)一个没有外接圆的五边形;(c)另一个没有外接圆的五边形
:::
例如,图 E.2(a) 展示了一个五边形,其边长分别为 $3$、$1$、$6$、$1$ 和 $7$ 个单位,代表 $3$ 月 $16$ 日和 $17$ 日。该圆的半径约为 $3.544$ 个单位。图 E.2(b) 和图 E.2(c) 展示了具有相同边长的五边形,但它们都没有外接圆。
为了将珠宝商业化,她需要能够根据指定的边长计算出外接圆的半径。你能通过编写一个程序来完成这个任务来帮助她吗?
输入格式
输入包含单个测试用例,格式如下。
$$
\begin{aligned}
&n\\
&x_1 \cdots x_n\\
\end{aligned}
$$
$n$ 是一个整数,表示边的数量($3 \le n \le 1000$)。$x_k$ ($k = 1, \dots, n$)是一个整数,表示第 $k$ 条边的长度($1 \le x_k \le 6000$)。
你可以假设存在一个或多个具有指定边长的多边形。你可以证明,这样的多边形中至少有一个拥有外接圆。
输出格式
输出一个具有指定边长的多边形的最小外接圆半径。输出的绝对误差或相对误差应在 $10^{-7}$ 以内。