P14871 [ICPC 2020 Yokohama R] LCM of GCDs

时间限制：10s -> 2s

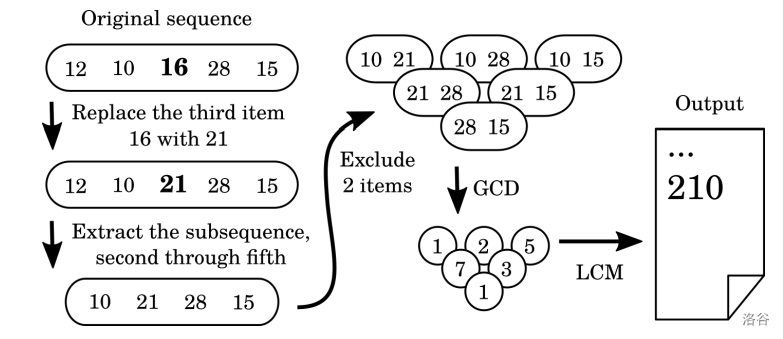
给定一个正整数序列，随后是一系列指令，这些指令指定了对序列的更新以及需要回答的查询。更新和查询以任意顺序给出。 每个更新操作将序列中的一个元素替换为给定值。更新是累积的：后续所有指令都基于指定替换后的序列。 每个查询指定一个（可能更新后的）序列的子序列，以及要从该子序列中排除的元素数量。根据排除哪些元素，将产生一个或多个整数集合。每个这样的集合有其成员的最大公约数（GCD）。查询的答案就是所有这些集合的 GCD 的最小公倍数（LCM）。 :::align{center}  图 H.1. 解答样例输入 1 中最后一个查询 “Q 2 5 2” :::

输入包含单个测试用例，格式如下。 $$ \begin{aligned} &n \ m \\ &a_1 \ldots a_n \\ &c_1 \\ &\vdots \\ &c_m \end{aligned} $$ 第一行有两个整数 $n$ 和 $m$。$n$ （$1 \le n \le 10^5$）是整数序列的长度，$m$ （$1 \le m \le 10^5$）是指令的数量。第二行给出了原始的整数序列 $a_1, \ldots, a_n$。对于 $i = 1, \ldots, n$，有 $1 \le a_i \le 10^6$。接下来的 $m$ 行中，每行要么是一个以字母 U 开头的更新指令，要么是一个以字母 Q 开头的查询指令。 更新指令的格式如下。 $$ \begin{aligned} &\text{U } j \ x \end{aligned} $$ 该指令表示将序列的第 $j$ 个元素替换为整数 $x$。满足 $1 \le j \le n$ 且 $1 \le x \le 10^6$。更新是累积的：以下所有指令都基于更新后的序列。 查询指令的格式如下。 $$ \begin{aligned} &\text{Q } l \ r \ k \end{aligned} $$ 其中，$l$ 和 $r$ 指定了一个子序列的起始和结束位置，$k$ 是要从该子序列中排除的元素数量。子序列为 $b_l, \ldots, b_r$，这里 $b_1, \ldots, b_n$ 是在应用该查询之前的所有更新后得到的序列。满足 $1 \le l$，$0 \le k \le 2$，且 $l + k \le r \le n$。

对于更新指令，不需要输出。对于每个查询指令，输出一行，该行内容是：从序列 $b_l, \ldots, b_r$ 中排除 $k$ 个元素形成的所有子序列对应的整数集合，计算每个集合的 GCD，再计算这些 GCD 的 LCM。

对于此测试用例的第一个查询 “Q 1 3 1”，子序列是 $12\ 10\ 16$。排除一个元素会产生三个元素集合：$\{12, 10\}$、$\{12, 16\}$ 和 $\{10, 16\}$。它们的 GCD 分别是 $2$、$4$ 和 $2$，因此输出应该是它们的 LCM，即 $4$。 注意，第五个指令给出的更新 “U 3 21” 改变了后续相同查询 “Q 1 3 1”（即第六个指令）的答案。该更新使子序列变为 $12\ 10\ 21$。因此，排除一个元素后得到的集合是 $\{12, 10\}$、$\{12, 21\}$ 和 $\{10, 21\}$。它们的 GCD 分别是 $2$、$3$ 和 $1$，所以这个查询的输出应该是它们的 LCM，即 $6$。