P14879 [ICPC 2019 Yokohama R] Reordering the Documents

Susan 擅长为了便利而布置餐桌，但不擅长整理办公桌。 Susan 刚完成了一组文件的文书工作，这些文件仍然堆在她的桌子上。它们有序列号，并且当她的老板拿进来时**原本**是按顺序堆叠的。然而，由于她太懒而没有将滑出文件堆的文件放回正确位置，现在的顺序并不完美。听到她已完成工作，老板希望她立即将他送来的文件盒中的文件归还。当然，文件应按其序列号的顺序存放在盒子中。 桌子上的空间刚好够再放两堆文件，Susan 计划在这两个位置制作两个临时文件堆。当前文件堆中的所有文件都将逐个从顶部移动到两个临时文件堆之一。由于匆忙将文件堆得太高会导致它们倒塌，所以不应在临时堆上放置太多文件。在将**所有**文件移动到临时堆并收到文件盒后，两个堆中的文件将从顶部逐个移入盒子。为了使它们能按顺序移入盒子，两个堆中的文件应与其序列号相反的顺序排列。 例如，假设文件堆中有六份文件 $\#1$、$\#3$、$\#4$、$\#2$、$\#6$ 和 $\#5$，从上到下按此顺序排列，并且临时文件堆不能超过三份文件。那么，她可以形成两个临时文件堆，一个从上到下是 $\#6$、$\#4$ 和 $\#3$，另一个是 $\#5$、$\#2$ 和 $\#1$（图 E.1）。两个临时文件堆都是逆序排列的。然后，比较两个临时文件堆顶部的文件序列号，数字较大者（本例中是 $\#6$）将首先被取出并存放到文件盒中。重复此过程，所有文件将在文件盒中完美排序。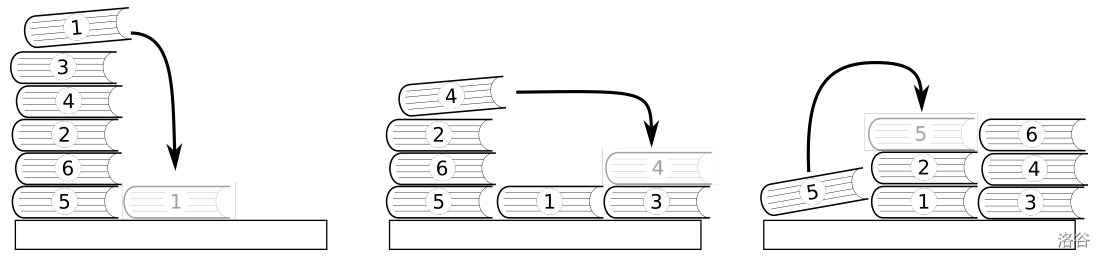 :::align{center}  图 E.1. 制作两个临时文件堆 ::: Susan 想知道，对于当前文件堆中的文件，该计划是否实际可行，如果可行，有多少种不同的方式将它们堆叠到两个临时文件堆中。你被要求通过编写一个程序来计算不同方式的数量来帮助 Susan，如果计划不可行，则该数量应为零。 由于文件堆中的每个文件都可以移动到两个临时文件堆中的任意一个，对于 $n$ 份文件，总共有 $2^n$ 种不同的选择组合，但其中一些可能会破坏临时文件堆的逆序，因此是不合适的。 上述示例对应于样例输入的第一个案例。在这种情况下，最后两份文件 $\#5$ 和 $\#6$ 可以交换它们的目的堆。此外，完全交换两个临时文件堆的角色也是可行的。由于任何其他移动序列都会使其中一个堆高于三份文件和/或使它们顺序混乱，因此在此示例中，将文件堆叠到临时堆的不同方式总数为 $2 \times 2 = 4$。

输入包含单个测试用例，格式如下。 $$ \begin{aligned} &n\ m\\ &s_1 \dots s_n\\ \end{aligned} $$ 其中，$n$ 是文件堆中的文件数量（$1 \le n \le 5000$），$m$ 是一个临时文件堆在不冒倒塌风险的情况下可以堆叠的文件数量（$n/2 \le m \le n$）。数字 $s_1$ 到 $s_n$ 是文件堆中文件的序列号，从顶部到底部。保证所有数字 $1$ 到 $n$ 都恰好出现一次。

输出一行一个整数，表示形成两个适合目标的临时文件堆的方式数量。当然，如果没有可行的选择，方式数量为 $0$。 如果可能的方式数量大于或等于 $10^9 + 7$，则输出方式数量对 $10^9 + 7$ 取模的结果。