P14884 [ICPC 2019 Yokohama R] Fun Region
题目描述
Ciel 博士居住在一个海岸线为多边形的平面岛屿上。她喜欢沿着螺旋路径在岛上散步。这里,一条路径被称为**螺旋**路径,如果它满足以下两个条件。
- 该路径是一条简单的平面折线,没有自相交。
- 在其所有顶点处,线段方向均为顺时针转向。
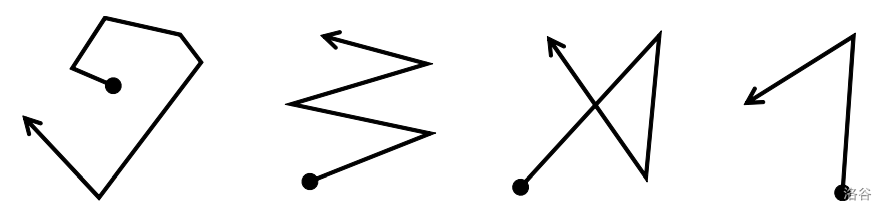
下图描绘了四条路径。圆圈标记表示起点,箭头表示路径的终点。在这些路径中,只有最左边的是螺旋路径。
:::align{center}
:::
Ciel 博士认为一个点具有**乐趣**,如果对于岛屿海岸线的所有顶点,都存在一条螺旋路径从该点出发,到达该顶点,且不穿越海岸线。这里,螺旋路径可以接触或重叠于海岸线。
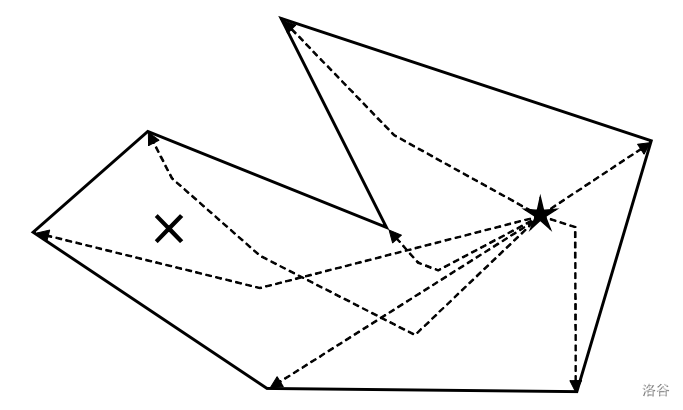
在下图中,外多边形代表海岸线。点 $\star$ 具有乐趣,而点 $\times$ 不具有乐趣。从 $\star$ 出发的虚线折线是有效的螺旋路径,终点为海岸线顶点。
:::align{center}
:::
:::align{center}
:::
我们可以证明,所有具有乐趣的点构成一个(可能为空的)连通区域,我们称之为**乐趣区域**。给定海岸线,你的任务是编写一个程序来计算乐趣区域的面积大小。
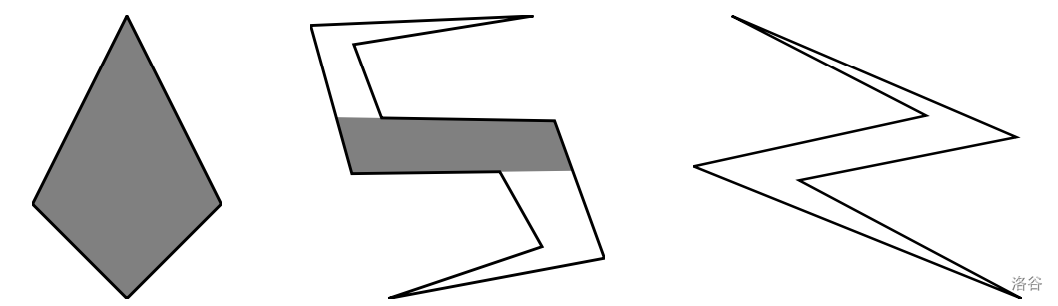
图 J.1 可视化了下文给出的三个样例。外多边形对应于岛屿的海岸线。乐趣区域显示为灰色区域。
输入格式
输入包含单个测试用例,格式如下。
$$
\begin{aligned}
&n \\
&x_1 \ y_1 \\
&\vdots \\
&x_n \ y_n
\end{aligned}
$$
$n$ 是表示海岸线的多边形的顶点数($3 \le n \le 2000$)。接下来的 $n$ 行中,每行有两个整数 $x_i$ 和 $y_i$,它们给出了多边形第 $i$ 个顶点的坐标 $(x_i, y_i)$,按逆时针顺序排列。$x_i$ 和 $y_i$ 介于 $0$ 到 $10000$ 之间(含)。这里,坐标系的 $x$ 轴指向右,$y$ 轴指向上。多边形是简单的,即它不自交也不自触。注意,多边形可能是非凸的。保证每个顶点的内角不等于 $180$ 度。
输出格式
在一行中输出乐趣区域的面积。允许的绝对误差或相对误差小于 $10^{-7}$。