P14895 [ICPC 2018 Yokohama R] Emergency Evacuation

日本政$ $府计划在 $2020$ 年将入境游客数量增加到四千万，并在 $2030$ 年增加到六千万。要实现这样的数字，不仅需要增加旅游吸引力，进一步发展旅游基础设施也是必不可少的。 在交通方面，一个可能的改进是提供极长和/或极宽的车辆，一次运送许多乘客。然而，过大的车辆在紧急情况下疏散所有乘客可能需要很长时间。你被请求帮助估算所需的时间。 假设车辆具有以下座位布局。 - 一条中央过道笔直穿过车辆，直接连接到车辆后部中央的紧急出口门。 - 过道两侧有相同数量的乘客座位排。 所请求的粗略估算基于一个简单的逐步模型。所有乘客最初都位于不同的座位上，他们在每一步中可以执行以下一种移动。 - 座位上的乘客可以向靠近过道的相邻座位移动。靠近过道的座位上的乘客可以直接横向移动到过道上。 - 过道上的乘客可以向后移动一排座位。如果乘客在紧急出口前方（即最后一排座位处），他/她可以下车。 要移动到的座位或过道位置必须是空的；即在该步骤之前没有其他乘客在那里，或者在那里的乘客通过在同一步骤中移动到另一个位置而腾出了该位置。当两个或更多乘客满足同一位置的移动条件时，只有其中一人可以移动，其他人必须在原位置等待。 图 C.1 中最左边的图描绘了样例输入 1 中给出的一个小型车辆的座位布局。该车辆有五排座位，过道两侧各有两个座位，总共二十个座位。车上七名乘客的初始位置也已标出。 图 C.1 中的另外两个图显示了第一步和第二步之后乘客的可能位置。乘客移动用粗箭头表示。请注意，前排座位上的两名乘客在第一步中不得不等待空位，第二排的一名乘客在下一步中不得不等待。 你的任务是编写一个程序，在给定座位布局和乘客初始位置的情况下，计算出所有乘客下车所需的最小步数。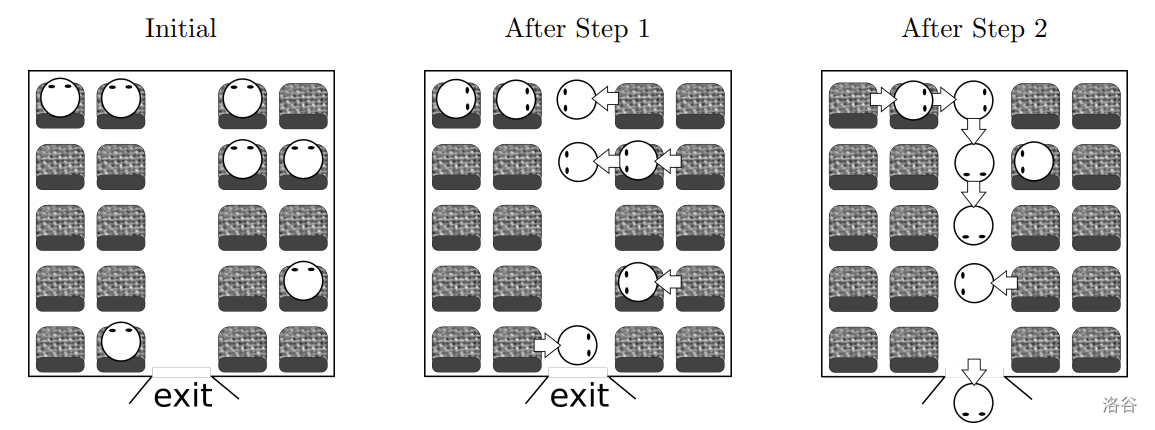 :::align{center}  图 C.1. 简单模型 :::

输入包含单个测试用例，格式如下。 $$ \begin{aligned} & r \quad s \quad p \\ & i_1 \quad j_1 \\ & \vdots \\ & i_p \quad j_p \end{aligned} $$ 其中，$r$ 是乘客座位排数，$s$ 是过道每侧的座位数，$p$ 是乘客数量。它们是满足 $1 \leq r \leq 500$，$1 \leq s \leq 500$ 和 $1 \leq p \leq 2rs$ 的整数。 接下来的 $p$ 行给出乘客的初始座位位置。第 $k$ 行包含 $i_k$ 和 $j_k$，表示第 $k$ 个乘客的座位在第 $i_k$ 排，且是该排的第 $j_k$ 个座位。这里，排数和座位编号均从前到后、从左到右计数，且都从 $1$ 开始。它们满足 $1 \leq i_k \leq r$ 和 $1 \leq j_k \leq 2s$。乘客位于不同的座位上，即如果 $k \neq l$，则 $i_k \neq i_l$ 或 $j_k \neq j_l$ 成立。

输出应包含一行一个整数，表示所有乘客下车所需的最小步数。