P14898 [ICPC 2018 Yokohama R] Fair Chocolate-Cutting

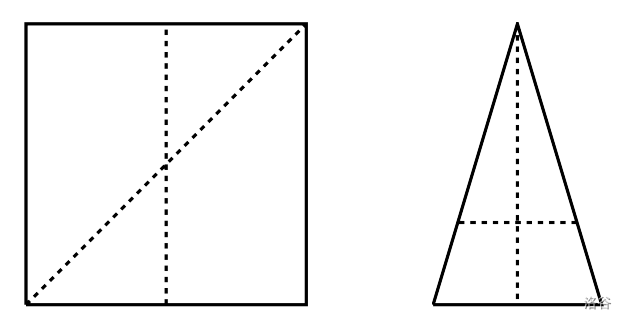
你有一块凸多边形形状的平面巧克力。你需要用一把直刀将其切成两块面积完全相同的部分。 对于给定的凸多边形，编写一个程序，计算将该多边形分割成两个相等面积的线段的最大长度和最小长度。 下图对应于前两个样例输入。每个图中的两条虚线分别对应最小和最大长度的等面积切割线。 :::align{center}  图 F.1. 样例巧克力块及切割线 :::

输入包含单个测试用例，格式如下。 $$ \begin{aligned} & n \\ & x_1 \quad y_1 \\ & \vdots \\ & x_n \quad y_n \end{aligned} $$ 第一行有一个整数 $n$，表示给定多边形的顶点数。其中，$n$ 在 $3$ 到 $5000$ 之间（含）。接下来的 $n$ 行中，每行有两个整数 $x_i$ 和 $y_i$，它们按逆时针顺序给出了多边形第 $i$ 个顶点的坐标 ($x_i$, $y_i$)。$x_i$ 和 $y_i$ 都在 $0$ 到 $100000$ 之间（含）。 保证多边形是简单且凸的。换句话说，多边形的任意两条边互不相交，且其所有顶点的内角都小于 $180^\circ$。

应输出两行。第一行应包含将多边形分割成两个相等面积的直线段的最小长度。第二行应包含此类直线段的最大长度。如果输出的值与正确答案的绝对误差或相对误差小于 $10^{-6}$，则视为正确。