P14904 [NHSPC 2024] 計程車叫車問題

你是某計程車公司老闆，擁有 $m$ 台計程車。這些計程車都在 $x$ 軸上，位置分別是 $t_1, t_2, t_3, \ldots,t_m$。同時，你接到 $m$ 名路人的搭車請求，這 $m$ 名路人也在 $x$ 軸上，位置分別是 $p_1, p_2, p_3, \ldots, p_m$。我們假設上述 $2m$ 個座標均相異。你的任務是為每一位路人指派一台計程車，且每台計程車只能指派給一位路人。你的目標是最小化這 $m$ 台計程車到其指派路人的距離總和（稱此距離總和為叫車距離總和）。你的程式必須輸出最小叫車距離總和。 舉例來說，如果你有 $2$ 台計程車（$m=2$），位置分別在 $100$ 與 $1$（$t_1=100, t_2=1$），而 $2$ 名路人位置分別在 $3$ 與 $101$（$p_1=3, p_2=101$），則最小叫車距離總和為 $|100-101|+|1-3|=3$。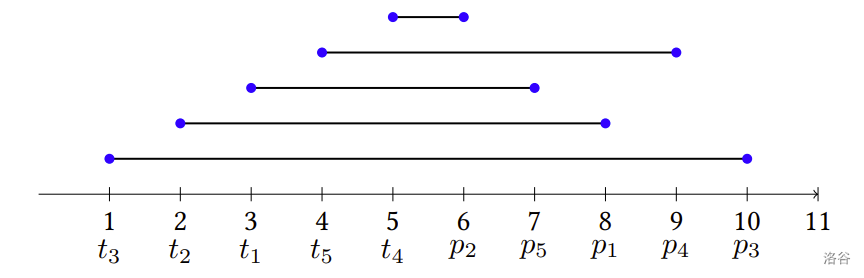 下圖顯示另一個例子。在這個例子中有$5$台計程車（$m=5$），位置分別在 $3, 2, 1, 5, 4$（$t_1=3, t_2=2, t_3=1, t_4=5, t_5=4$），而 $5$ 名路人位置分別在 $8, 6, 10, 9, 7$（$p_1=8, p_2=6, p_3=10, p_4=9, p_5=7$），則最小叫車距離總和為 $25$（下圖所顯示的計程車指派方式之叫車距離總和即為 $25$）。 :::align{centered}  :::

$$ \begin{aligned} &m \\ &t_1 \ t_2 \ \ldots \ t_m \\ &p_1 \ p_2 \ \ldots \ p_m \end{aligned} $$ * $m$ 代表路人及計程車的數量。 * $t_i$ 代表第 $i$ 輛計程車的位置。 * $p_i$ 代表第 $i$ 個路人的位置。

$$a$$ * $a$ 代表給定輸入的最小叫車距離總和。

### 測資限制 * $1 \leq m \leq 10^6$。 * $1 \leq t_i \leq 2 \times 10^6$。 * $1 \leq p_i \leq 2 \times 10^6$。 * 保證給定的 $2m$ 個座標均相異。 ### 評分說明 本題共有兩組子任務，條件限制如下所示。 每一組可有一或多筆測試資料，該組所有測試資料皆需答對才會獲得該組分數。 | 子任務 | 分數 | 額外輸入限制 | | :------: | :----: | ------------ | | 1 | 40 | $\max_i\{t_i\} < \min_i\{p_i\}$。 | | 2 | 60 | 無額外限制。 |