P14907 [NHSPC 2024] 蓋蓋樂

$\textcolor{red}{\textbf{本題為 Output Only。}}$

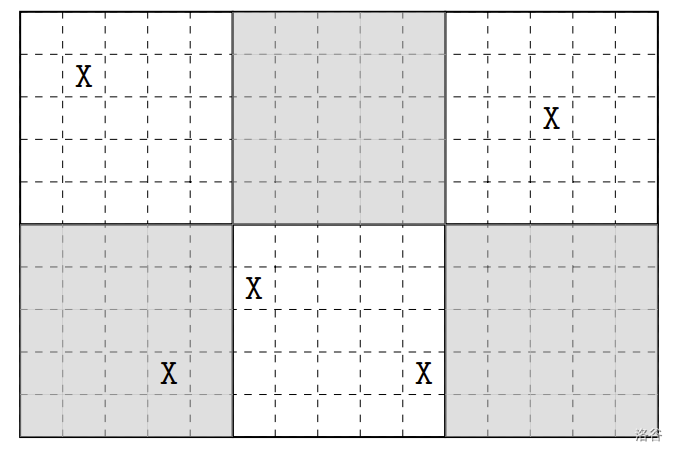
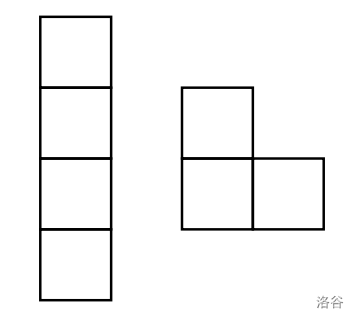
蓋蓋樂是一人策略遊戲。給定一個大棋盤，棋盤分成 $m\times n$ 個區塊，相鄰區塊分別塗上白色與灰色以做區隔。每個區塊都是個 $5\times 5$ 的方形小棋盤，每個小棋盤最多會有 $2$ 個特殊的格子。舉例來說，下圖是一個 $2\times 3$ 的大棋盤 $(m = 2, n = 3)$，其中有五個格子是特殊格子（以 $\texttt{X}$ 標示）。 :::align{center}  ::: 蓋蓋樂有兩種積木（如下圖所示），分別可用以蓋住棋盤上 $4$ 或 $3$ 個格子。兩種積木分別可以任意旋轉 $0, 90, 180, 270$ 度後再蓋住棋盤格子，但是特殊的格子不可以被蓋住。 :::align{center}  ::: 請用以上兩種積木把大棋盤蓋滿（特殊格子除外），使得**共用積木的區塊對**越少越好。 * 也就是說，只要有兩個區塊共用了同一塊積木，無論他們共用了幾塊，都會被算做一個「共用積木的區塊對」。你的目標就是最小化這個區塊對的數量。 在本題中，保證任意兩個特殊格子**皆不八方位相鄰**。也就是說，對於任兩個特殊格子座標 $(a, b), (c, d)$，皆有 $\max(|a - c|, |b - d|) > 1$。

$$\begin{aligned} &n \ m \\ &a_{1, 1} \ a_{1, 2} \ \cdots \ a_{1, 5m} \\ &a_{2, 1} \ a_{2, 2} \ \cdots \ a_{2, 5m} \\ &\vdots \\ &a_{5n, 1} \ a_{5n, 2} \ \cdots \ a_{5n, 5m} \end{aligned}$$ * $n, m$ 為棋盤的大小。 * $a_{i, j}$ 代表棋盤第 $i$ 列第 $j$ 欄的格子是否為特殊格子（也就是不能被蓋住的格子），以 $0$ 或 $-1$ 表示，其中 $0$ 代表可被蓋住的棋盤格子，$-1$ 代表特殊的格子。

$$\begin{aligned} & b_{1, 1} \ b_{1, 2} \ \cdots \ b_{1, 5m} \\ & b_{2, 1} \ b_{2, 2} \ \cdots \ b_{2, 5m} \\ & \vdots \\ & b_{5n, 1} \ b_{5n, 2} \ \cdots \ b_{5n, 5m} \end{aligned}$$ 請將棋盤蓋滿（特殊格子除外）後送回評分。積木蓋住棋盤的表示方式如下: * 同一塊積木需以相同的**正整數**作為代號，例如 $1, 2, 3, \ldots$，但代號最大不可超過 $15000$。特殊格子必須維持以 $-1$ 代表之。 * 不同塊積木**不可以**使用相同的代號。

### 範例 作為範例，假設測試資料的長相為 ``` 2 3 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 -1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 -1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 -1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 -1 0 0 0 0 0 -1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 ``` 則下面是一個可能的合法輸出 ``` 1 1 2 2 3 3 11 12 12 12 12 21 21 21 21 1 -1 2 4 3 13 11 11 14 15 15 15 15 22 22 5 5 6 4 4 13 13 16 14 14 23 23 -1 22 24 5 7 6 6 8 8 17 16 16 18 23 25 25 24 24 9 7 7 10 8 19 17 17 20 18 18 25 26 27 27 9 9 28 10 10 19 19 35 20 20 41 26 26 27 42 29 29 28 28 30 -1 36 35 35 37 41 41 43 42 42 29 31 32 32 30 30 36 36 38 37 37 43 43 44 44 31 31 32 -1 33 33 39 38 38 -1 45 45 45 45 44 34 34 34 34 33 39 39 40 40 40 40 46 46 46 46 ``` 在這個範例中，最佳解的共用積木區塊對數量為 $1$，而上面輸出的任兩個相鄰區塊都有共用積木，得到區塊對數量為 $7$，表示 $p$ 和 $q$ 的值分別為 $1$ 和 $7$。因此，假設分數比重 $S=10$，這個輸出可以獲得 $S\cdot\max\left(\frac{1}{10}, \frac{1}{\sqrt{7 - 1 + 1}}\right) \approx 3.78$ 分。 ### 視覺化工具（Visualizer） 為了方便選手觀看自己的輸出結果以及觀察測試資料，在此任務的附件（attachment）中，有一腳本程式（script）供選手視覺化（visualize）輸入檔與輸出檔。 請利用下列指令視覺化輸入檔。 ``` python3 visualizer.py [input file] ``` 你可利用下列指令，將你對於某個輸入計算出的解做視覺化。因為技術上的限制，附件中提供的視覺化工具在棋盤過大時，僅會顯示前 $10$ 排、以及前 $10$ 欄的方形小棋盤。 ``` python3 visualizer.py [input file] --solution [output file] ``` 為了方便辨識，程式會以上色每塊積木的方式輸出，而不輸出積木上面的數字。但由於顏色數量有限，程式會重新為所有積木上色並僅保證相鄰的積木不同色。 範例： ``` python3 visualizer.py input_1_1.txt --solution output_1_1.txt ``` 請注意，若你傳入的資料的格式並不合法，將會產生一些不可預期的行為。不過，當你的解答唯一違反的規則是「未蓋滿所有格子」時，將未被蓋到的格子留下數字 $0$ 會讓該格子呈現白色，並正常的進行視覺化。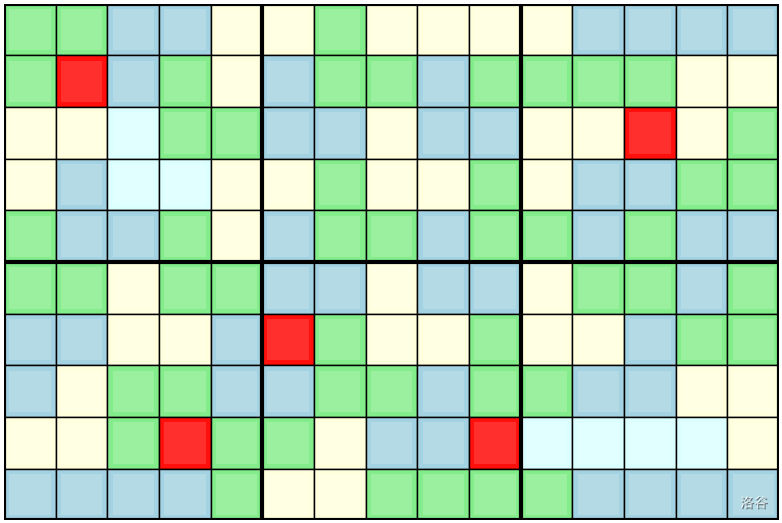 一張使用前面範例所提到的視覺化成果圖如下： :::align{center}  ::: ### 測資限制 * $1\le n\times m\le 1600$。 * $-1 \leq a_{i, j} \leq 0$。 * 輸入的數字皆為整數。 * 保證任一個被劃分出來的 $5\times 5$ 方形小棋盤內，特殊格子數量都不超過 $2$。 * 保證存在一種可以蓋滿棋盤的方式。 * 保證任意兩個特殊格子皆不八方位相鄰。 ### 評分說明 本題共有 10 組測試資料，輸入檔案的說明如表所示。 對於每一組測試資料，若你上傳的輸出檔案滿足輸出格式，並且成功蓋滿了所有除了特殊格子以外的格子，那麼你會得到以下分數 $$ S \cdot \max\left(\frac{1}{10}, \frac{1}{\sqrt{q - p + 1}}\right) $$ 其中 $S$ 是該測試資料的分數比重，$p$ 是最佳解的共用積木區塊對數量、$q$ 是你給出的構造內的共用積木區塊對數量。 若你上傳的輸出檔案不滿足輸出格式、或是沒有蓋滿所有除了特殊格子以外的格子，那麼你將得到 $0$ 分。 | 測試資料 | 分數比重 $S$ | 輸入檔名 | 輸出檔名 | 說明 | | :------: | :----: | :----: | :----: | ------------ | | 1 | 4 | `input_1_1.txt` | `output_1_1.txt` | $n = 1$，$m = 1$。| | 2 | 4 | `input_2_1.txt` | `output_2_1.txt` | $n = 1$，$m = 2$。| | 3 | 6 | `input_3_1.txt` | `output_3_1.txt` | $n = 1$，$m = 3$。| | 4 | 8 | `input_4_1.txt` | `output_4_1.txt` | $n = 2$，$m = 2$。| | 5 | 10 | `input_5_1.txt` | `output_5_1.txt` | $n = 10$，$m = 10$。| | 6 | 12 | `input_6_1.txt` | `output_6_1.txt` | $n = 10$，$m = 10$。| | 7 | 8 | `input_7_1.txt` | `output_7_1.txt` | $n = 1$，$m = 1599$。| | 8 | 20 | `input_8_1.txt` | `output_8_1.txt` | $n = 20$，$m = 24$。| | 9 | 20 | `input_9_1.txt` | `output_9_1.txt` | $n = 40$，$m = 40$。| | 10 | 8 | `input_10_1.txt` | `output_10_1.txt` | $n = 39$，$m = 39$。|