P14910 [NHSPC 2024] 實境節目

Ray 是某超大型實境節目的負責人。在節目開始不久，他就發現了有 $n_0$ 位參賽者非常擅長社交，這 $n_0$ 位參賽者已經**和所有參賽者建立了關係**。Ray將這 $n_0$ 位參賽者稱為「中心圈圈」，代號 $K_0$。 隨著節目進展到中期，中心圈圈以外的參賽者們也逐漸形成了各自的「小圈圈」。Ray 觀察到總共有 $t$ 個小圈圈，代號 $K_1, K_2, \ldots, K_t$，並且這些小圈圈分別有 $n_1, n_2, \ldots, n_t$ 位參賽者。每位參賽者只會恰好屬於其中一個小圈圈或是中心圈圈。而Ray之所以把它稱為小圈圈是因為對於所有屬於小圈圈 $K_i$ $(1 \leq i \leq t)$ 的參賽者而言，他們**只有和屬於相同小圈圈 $K_i$ 以及中心圈圈 $K_0$ 的所有參賽者建立關係**。 為了方便解釋，下面會用圖來表示這個實境節目，每個節點分別代表一位參賽者，而任兩個節點之間有邊代表這兩位參賽者之間有建立關係，反之則沒有。 舉例來說，圖(a)上有一個中心圈圈 $K_0$，兩個小圈圈 $K_1$、$K_2$，$n_0=2$、$n_1=1$、$n_2=2$。假設中心圈圈的參賽者為 $\{\text{A}, \text{B}\}$，小圈圈的參賽者依序為 $\{\text{C}\}$、$\{\text{D}, \text{E}\}$，可以看到位於中心圈圈 $K_0$ 的參賽者和所有參賽者都有建立關係，相同小圈圈內的參賽者都有相互建立關係，並且對於分屬不同小圈圈 $K_i$、$K_j$ $(1 \leq i < j \leq t)$ 的任兩位參賽者而言，都沒有建立關係。圖(b)、(c)也是同樣正確的範例。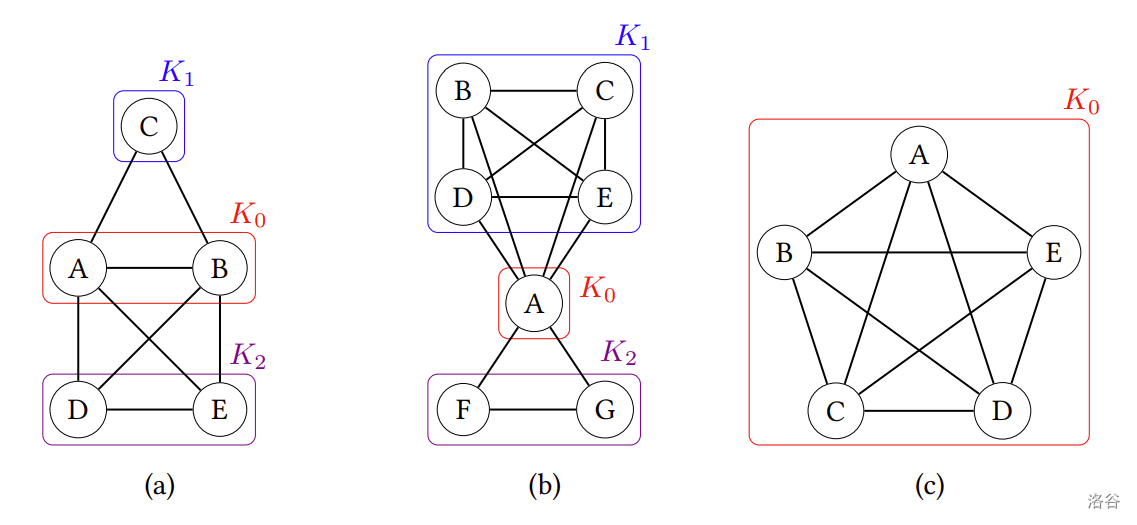 :::align{center}  ::: 而到了節目後期，Ray需要舉辦一場比賽，讓所有有建立關係的任兩位參賽者都進行一次對決，並且這些對決一定會有一方獲勝。如果參賽者 $x$、$y$ 進行對決並且 $x$ 贏得勝利，則我們稱 $x$ 比 $y$ 強；如果參賽者 $x$ 比 $y$ 強並且 $y$ 比 $z$ 強，則我們又稱 $x$ 比 $z$ 強。 為了能夠決定出最終贏家（可能有多個），Ray**不希望存在三位參賽者 $x$、$y$、$z$ 使得 $x$ 比 $y$ 強，$y$ 比 $z$ 強，但 $z$ 又比 $x$ 強**。 所以他需要先私下列出一份完整勝負關係，讓所有參賽者照著這份勝負關係進行對決，使得最終結果滿足他的要求。一份勝負關係若要被稱為完整勝負關係，那**對於任兩位有建立關係的參賽者，都必須在勝負關係中決定出勝方是誰**。 如果要用圖來表示勝負關係，那麼對於任兩位有建立關係的參賽者 $x$、$y$，如果 $x$、$y$ 有進行對決，那就讓 $x$、$y$ 之間的邊指向勝方，例如 $x$ 贏得勝利就是指向 $x$。 舉例來說，圖(d)就是一份符合要求的完整勝負關係，最終贏家為 C 和 E。圖(e)中的 B、E 有建立關係但沒有分出勝負，所以它不是一份完整的勝負關係。而圖(f)則是因為 A 比 C 強、C 比 B 強、但 B 又比 A 強，所以它沒辦法決定出最終贏家。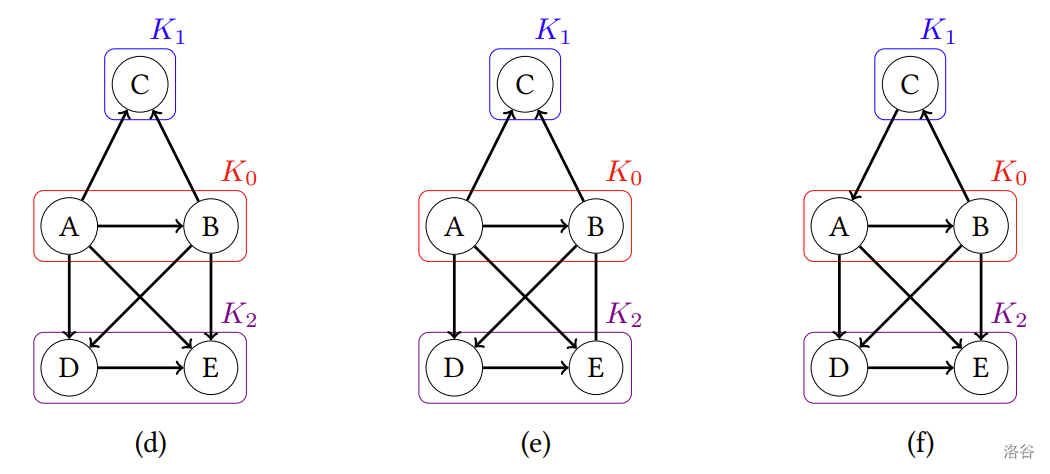 :::align{center}  ::: Ray 想要知道對於給定的超大型實境節目，總共有幾種符合要求的完整勝負關係。因為這個數字可能很大，你只要求出方法數除以 $10^9+7$ 的餘數就行了。

$$\begin{aligned} &t\\ &n_0 \ n_1 \ n_2 \ \ldots \ n_t \end{aligned}$$ * $t$ 代表小圈圈的數量。 * $n_0$ 代表屬於中心圈圈的參賽者人數。 * $n_i$ 代表屬於第 $i$ 個小圈圈 $K_i$ 的參賽者人數，$i \in \{1, 2, \ldots, t\}$。

$$ans$$ * $ans$ 代表符合要求的完整勝負關係的數量 mod $10^9+7$ 後的結果。

### 測資限制 * $0 \leq t \leq 10^6$。 * $1 \leq n_i \leq 10^7$。 * 輸入的數皆為整數。 ### 評分說明 本題共有四組子任務，條件限制如下所示。 每一組可有一或多筆測試資料，該組所有測試資料皆需答對才會獲得該組分數。 | 子任務 | 分數 | 額外輸入限制 | | :----: | :----------------: | --------------- | | 1 | 4 | $t = 0$。 | | 2 | 9 | $t \leq 1$。 | | 3 | 22 | $t \leq 2$。 | | 4 | 65 | 無額外限制。 |