P15002 [UOI 2019 II Stage] 重大发现
题目描述
近日,波托科兰迪亚的居民发现了一块 $2 \times 2$ 的古老石板,上面写有四个数字 $A$、$B$、$C$ 和 $D$,排列如下:
:::align{center}
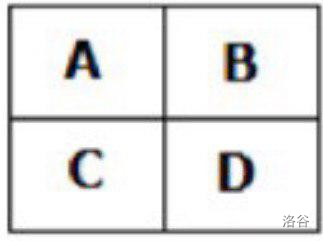
:::
他们立刻意识到,这是一项极其重要的历史发现。首先,他们将它交给了哥萨克胡子,让他来鉴定这块石板的重要性。哥萨克胡子认为,石板的重要性等于 $A \cdot (B + C - D)$。
遗憾的是,石板的正确朝向尚不明确。因此,可能无法唯一确定其重要性,因为这个值取决于它被旋转的次数。
假设一次旋转是指沿顺时针方向旋转 $90\degree$。
例如,若 $A = 41$、$B = 99$、$C = 100$、$D = 13$,则重要性为 $41 \cdot (99 + 100 - 13) = 7\,626$。但如果将其旋转一次,则重要性变为 $100 \cdot (41 + 13 - 99) = -4\,500$。
:::align{center}
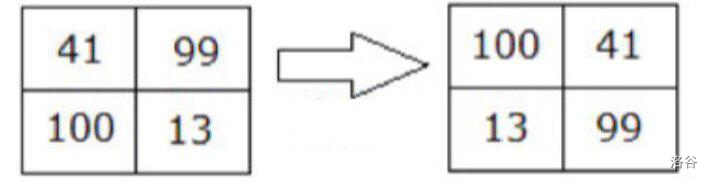
:::
哥萨克胡子想要确定这一发现可能具有的最大重要性。但他请你帮忙找出,为了使石板的重要性达到最大,最少需要进行多少次旋转。
输入格式
第一行包含四个整数 $A$、$B$、$C$ 和 $D$($-10^8 \le A, B, C, D \le 10^8$)—— 即石板上所写的数字。
输出格式
输出哥萨克胡子为了使石板的重要性达到最大,所需进行的最少旋转次数。
说明/提示
在第一个样例中,初始时石板的重要性为 $5$,但如果旋转一次,它将获得最大值的重要性,即 $32$。
在第二个样例中,需要旋转三次,石板才能达到其最大重要性值,即 $171$。
在最后一个样例中,石板无需旋转,因为它已经具有最大值的重要性,即 $18$。
除样例测试点外的每个测试点,分值为 $5$ 分。
翻译由 DeepSeek V3 完成