P15017 [UOI 2020 II Stage] 大炮

在通过考试后，哥萨克胡子决定去一个洞穴探险。为了让旅途更有趣，他决定用大炮作为交通工具。 洞穴内的路径长度为 $n$ 米，并划分为 $n$ 段，每段长 $1$ 米。路段从路径起点到终点按顺序编号为 $1$ 到 $n$。每段路的上方一定高度处悬挂着一个钟乳石（钟乳石——圆柱形或圆锥形的矿物形成物，从洞穴或其他空洞的天花板垂下，或从类似桥梁的人造结构垂下（源自维基百科））。具体来说，第一段路的上方高度为 $a_1$，第二段为 $a_2$，……，第 $n$ 段为 $a_n$。在假设的第 $n+1$ 段路（即路径之后）处，有一面墙，占据了从地面到天花板的所有空间（即整条垂直线）。 在除最后一段外的每一段路上，他都放置了一门高度为 $1$ 的大炮。每一门炮都向上倾斜 $45$ 度角。然后，哥萨克胡子坐进第一门炮并开火。他沿着 $45$ 度角向前飞行，直到撞上钟乳石。接着，他垂直下落。请注意，即使哥萨克触碰到钟乳石的角（图中第二段路），他也会继续飞过去，即不会下落。假设他落在了第 $i$ 段路上。如果 $i$ 是最后一段路（即 $i=n$），那么他的娱乐活动就此结束。否则，他会跳入第 $i$ 段路上的大炮，再次把自己发射出去。这个过程重复进行，直到哥萨克到达第 $n$ 段路为止。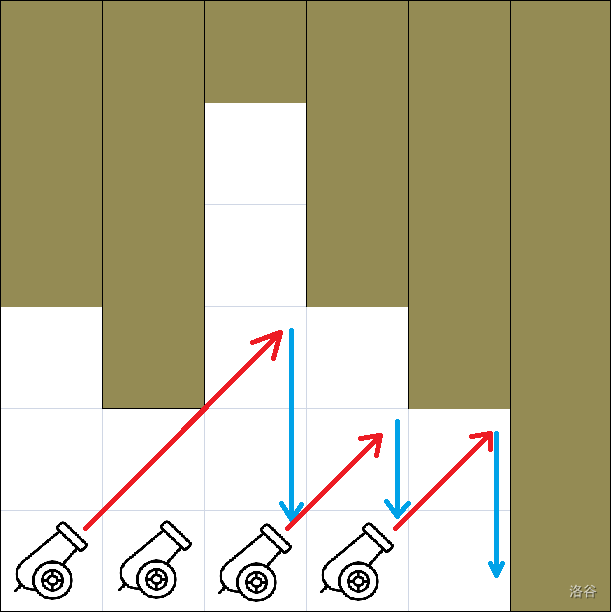 :::align{center}  第一个样例的示意图（红色表示发射后的飞行轨迹，蓝色表示撞到钟乳石后的下落轨迹） ::: 哥萨克胡子需要把自己发射多少次？

第一行包含一个整数 $n$ ($1 \leq n \leq 2 \cdot 10^5$) —— 路径长度。 第二行包含 $n$ 个整数 $a_1, a_2, \dots, a_n$ ($2 \leq a_i \leq 10^9$) —— 各路段的钟乳石悬挂高度。

输出一个数字 —— 哥萨克胡子需要进行的发射次数。