P15037 「chaynOI R2 T2」熟练地剖分
题目描述
flow 有一棵 $n$ 个点的**有根**树 $T$,根为 $1$,节点编号为 $1$ 至 $n$ 的正整数。
flow 想要构造一个新的**有根**树序列 $T_0=T,T_1,T_2,\dots$,满足 $T_{i+1}=f(T_i)$,对于所有 $i\ge 0$ 成立。
其中函数 $f(T)$ 定义如下(如有不理解,建议查看样例解释):
1. 定义一棵树 $T'$。
2. 对 $T$ 做[**树链剖分(重链剖分)**](https://oi-wiki.org/graph/hld/#%E9%87%8D%E9%93%BE%E5%89%96%E5%88%86),**若存在多个儿子子树大小相等则取儿子编号较小**的为重儿子。
3. 设第 $2$ 步中所有**重链**为 $L_1,L_2,\dots,L_k$,**则 $T'$ 中的所有点**编号为 $\{u\} = \{\min\limits_{v_1\in L_1}v_1,\min\limits_{v_2\in L_2}v_2,\dots,\min\limits_{v_k\in L_k}v_k\}$,可以证明,$L_i$ 的顺序不会改变最终 $T'$ 的结构。
4. **若对于 $i\ne j, \exist x\in L_i,y\in L_j$,且 $T$ 中存在一条边 $(x,y)$,则 $T'$ 中存在一条边** $(u_i,u_j)$,可以发现这样操作后 $T'$ 一定为一棵 $k$ 个结点的树。
5. **将 $T'$ 的根钦定为 $1$**(注意到一定存在一个 $i$ 使得 $u_i=1$),返回 $T'$。
flow 给定了你 $T$,flow 想让你求出一个**最小**的 $m$,使得 $\forall m'\ge m,T_{m'}=T_m$,可以证明,在本题范围内,$m\le10^9$。
输入格式
第一行一个整数 $n$。
第二行 $n-1$ 个整数 $fa_2,fa_3,\dots,fa_n$,表示在以 $1$ 为根的情况下,$2\sim n$ 的父亲节点。
输出格式
一行一个整数,表示 $m$。
说明/提示
### 样例 2 解释
一开始的 $T_0$ 为:
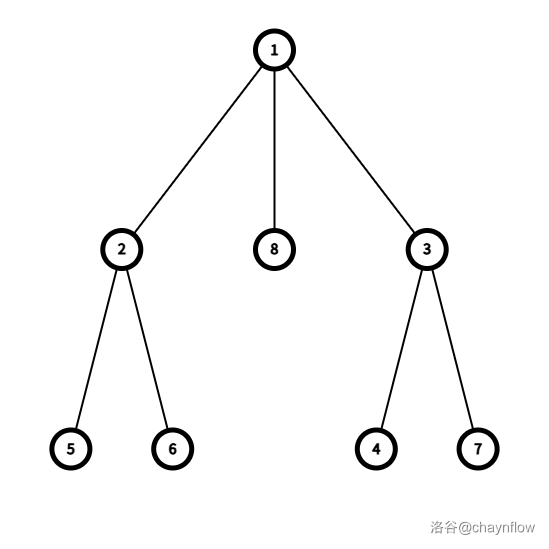
考虑 $f(T_0)$ 的过程:
1. $k=5,L_1=\{1,2,5\},L_2=\{6\},L_3=\{8\},L_4=\{3,4\},L_5=\{7\}$,注意 $L_i$ 的顺序其实不重要。
2. $T'$ 中的点: $\{u\}=\{1,6,8,3,7\}$。
3. $T'$ 中的边:$\{(1,3),(1,6),(1,8),(3,7)\}$。
+ 故 $T_1=f(T_0)$ 为:
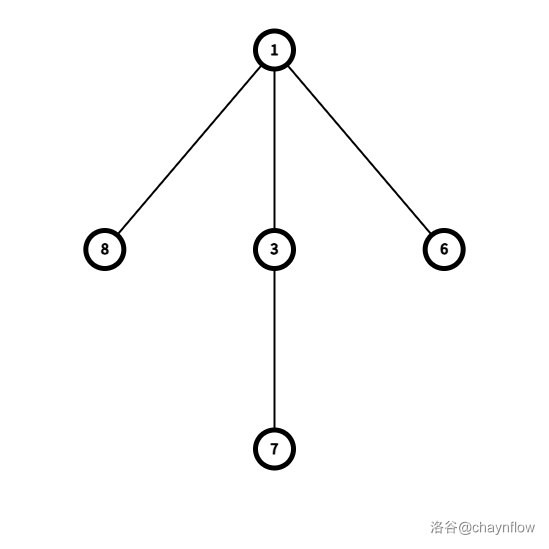
+ 同理可得,$T_2=f(T_1)$ 为:
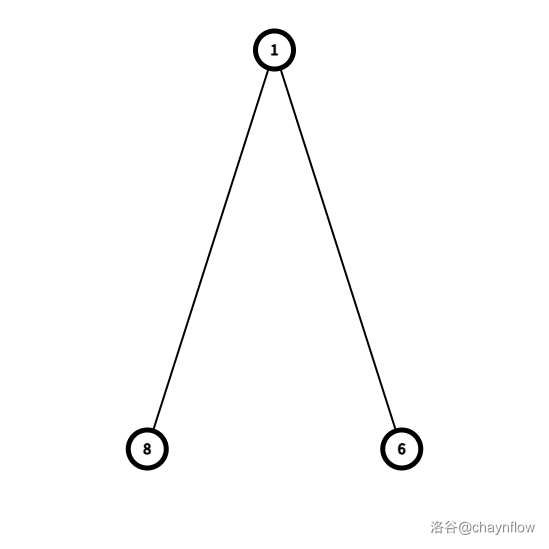
+ $T_3=f(T_2)$ 为:
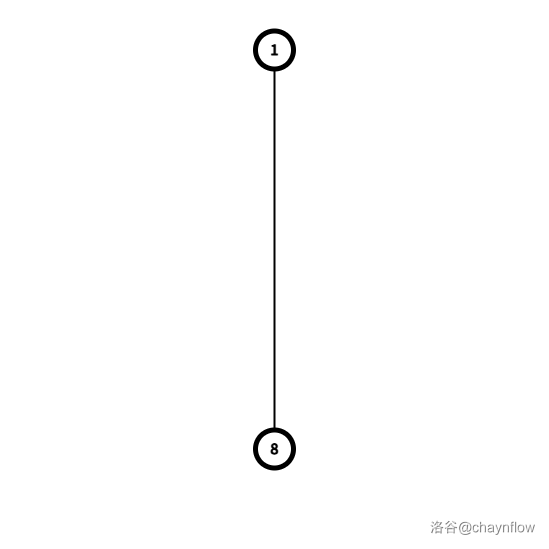
+ $T_4=f(T_3)$ 为:

+ $T_5=f(T_4)$ 为:

+ $T_6=f(T_5)$ 为······
注意到对于 $m'\ge 4$,$T_{m'}=T_4$,故最终 $m=4$。
### 数据范围
**请注意常数因子对程序运行效率带来的影响。**
对于 $100\%$ 的数据,$1\le n\le 5\times10^6$,$1\le fa_i