P15044 [UOI 2022 II Stage] 树

克索尼亚有一棵以顶点 $1$ 为根、包含 $n$ 个顶点的有根树，每个顶点上写有一个数字。在第 $i$ 个顶点上写有数字 $a_i$。 回忆一下，树是一种无环连通图。有根树是指在树中选择一个顶点作为根。 在有根树中，顶点 $v$ 的祖先是指从 $v$ 到根路径上的所有顶点（不包括顶点 $v$ 本身）。顶点 $v$ 的子树是指所有以 $v$ 为祖先的顶点集合，包括顶点 $v$ 本身。 集合 $S = (u_1, u_2, u_3, \dots, u_k)$ 的 XOR 和定义为数字 $u_1 \oplus u_2 \oplus u_3 \oplus \dots \oplus u_k$，其中 $\oplus$ 是按位异或操作，在 Pascal 语言中记为 `xor`，在 C++/Java/Python 语言中记为 `^`。 对于数字集合 $S$，考虑其所有可能子集的 XOR 和构成的集合。称此集合为 $F(S)$。 克索尼亚的朋友不断问她这样的问题——“如果考虑顶点 $v$ 的子树中所有数字的集合（记为 $U_v$），那么集合 $F(U_v)$ 中按升序排列的第 $k$ 个数是什么？”也就是说，如果取出顶点 $v$ 子树中的所有数字，考虑它们所有子集的 XOR 和，那么在得到的集合中，按升序排列的第 $k$ 个数是什么？如果不存在这样的数（即 $k > |F(U_v)|$），则克索尼亚回答数字 $-1$。请注意，$F(U_v)$ 是一个集合，而不是多重集。也就是说，如果一个数字出现多次，只应计入一次。 此外，克索尼亚的朋友有时会请她更改树中的一个数字。

第一行包含两个整数 $n, g$ ($2 \leq n \leq 5 \cdot 10^4$, $0 \leq g \leq 7$) —— 分别表示树中的顶点数量和测试组编号。 接下来的 $n - 1$ 行，每行包含两个整数 $x_i, y_i$ ($1 \leq x_i, y_i \leq n$)。这表示树中顶点 $x_i$ 和 $y_i$ 之间有一条边。保证该图是一棵树。 下一行包含 $n$ 个整数 $a_1, a_2, \dots, a_n$ ($0 \leq a_i < 2^{20}$) —— 表示树顶点上初始数字的数组 $a$。 下一行包含一个整数 $q$ ($1 \leq q \leq 5 \cdot 10^4$) —— 表示查询的数量。 接下来的 $q$ 行，每行描述一个查询。 更改树中数字的查询格式为 $1 \ x_i \ y_i$ ($1 \leq x_i \leq n$, $0 \leq y_i < 2^{20}$)。此类查询表示现在第 $x_i$ 个顶点上的数字变为 $y_i$。 另一种类型的查询格式为 $2 \ v_i \ k_i$ ($1 \leq v_i \leq n$, $1 \leq k_i \leq 10^9$)。此类查询需要找出集合 $F(U_{v_i})$ 中按升序排列的第 $k_i$ 个数，其中 $U_{v_i}$ 是顶点 $v_i$ 子树中的数字集合，$F(U_{v_i})$ 是其所有子集 XOR 和构成的集合。如果 $k_i > |F(U_{v_i})|$，则输出 $-1$。

对于每个第二类查询，在一个单独的行中输出答案。

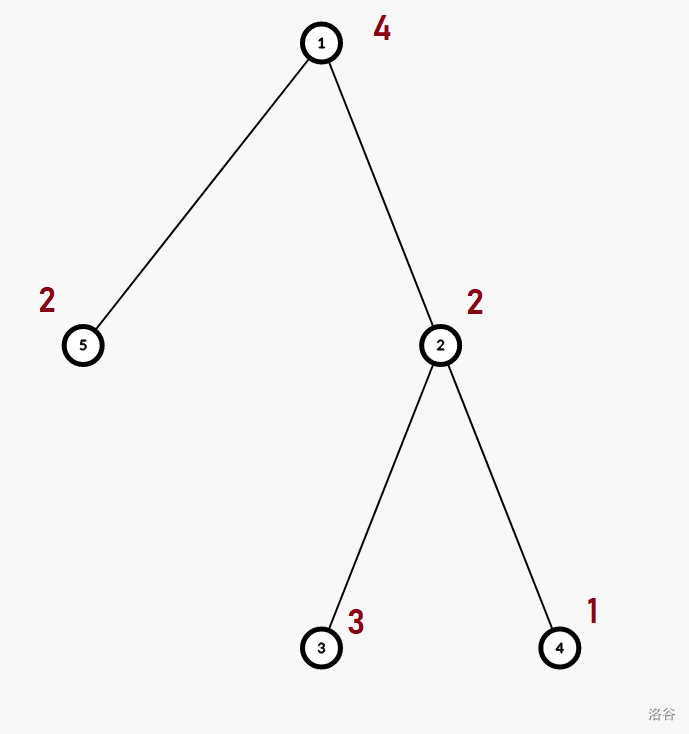
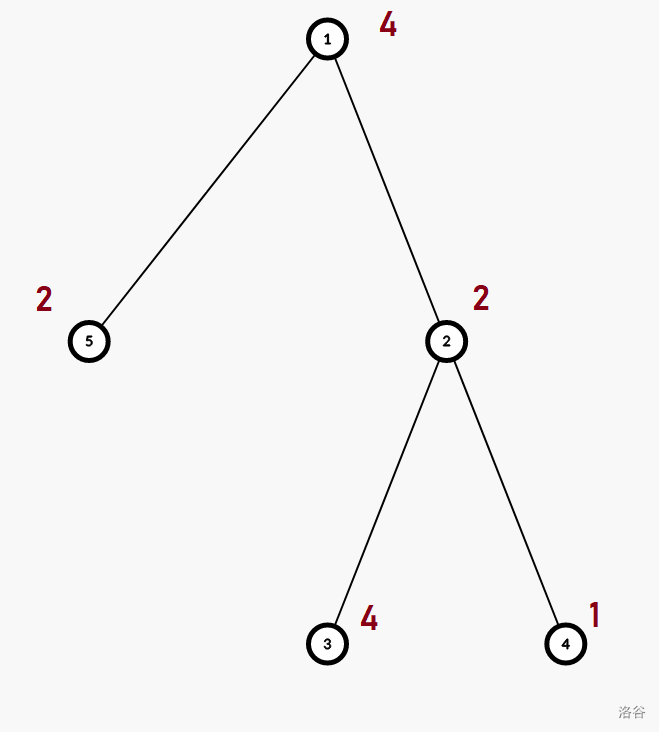
### 样例说明 第一个样例的解释。顶点旁的数字表示 $a_i$。 :::align{center}  ::: 在第一个查询中，考虑顶点 $2$ 的子树。它包含数字 $1, 2, 3$。 $F([1,2,3]) = [0, 1, 2, 3]$。 在第二个查询中，考虑整个子树。$F([1, 2, 3, 4]) = [0,1,2,3,4,5,6,7]$。 更改一个数字后，树的状态如下： :::align{center}  ::: 现在，顶点 $2$ 的子树中包含数字 $1, 2, 4$。 $F([1,2,4]) = [0,1,2,3,4,5,6,7]$。 ### 评分细则 - （6 分）： $q, n \leq 15$。 - （16 分）： $q, n \leq 500$。 - （18 分）： $q, n \leq 2000$。 - （7 分）： 在所有第二类查询中，$v_i = 1$。 - （13 分）： 没有更改数字的查询。 - （11 分）： 所有 $a_i, y_i$ 是 2 的幂。 - （29 分）： 无额外限制。 翻译由 DeepSeek V3 完成