P15053 [UOI 2023 II Stage] Land plots

Measuring a land plot is an important geodetic procedure. To obtain accurate numerical values, the measurement procedure should be performed by professional surveyors. Let us consider the following problem. Let us assume that there is a square plot that surveyors have divided into $n^2$ rectangular plots by drawing $(n-1)$ vertical and $(n-1)$ horizontal lines. Let us number the rows and columns of the small plots as shown on the picture (the scale is not respected). That is, the rows are numbered from bottom to top by integer numbers from $1$ to $n$; and the columns are numbered from left to right by integer numbers from $1$ to $n$. The plots located at the intersection of the $i$-th column and the $i$-th row $(1 \le i \le n)$ will be called the "main diagonal". The plots located at the intersection of the $(i+1)$-th column and the $i$-th row $(1 \le i \le n-1)$ will be called the "side diagonal". :::align{center}  ::: You know the areas of the plots on the main and side diagonals. Calculate the area of the plot at the intersection of the $p$-th column and the $q$-th row.

The first line contains an integer $n$ ($2 \le n \le 1\,000$). The second line contains $n$ integers $a_1, a_2, \dots, a_n$ ($1 \leq a_i \leq 10^9$) --- the areas of the plots on the main diagonal. The third line contains $n-1$ integers $b_1, b_2, \dots, b_{n-1}$ ($1 \leq b_i \leq 10^9$) --- the areas of the plots on the side diagonal. The fourth line contains two integers $p$ and $q$ ($1 \leq p, q \leq n$) --- the coordinates of the plot, the area of which should be calculated.

Output the area of the plot located at the intersection of the $p$-th column and the $q$-th row. We want to know the exact value of the area, so the answer should be given in a factorized form. In other words, the answer should be represented as several lines, each containing two integers $p_i$ and $s_i$: the number $p_i$ is necessarily prime, all $p_i$ are different, and the number $s_i$ is an integer and not equal to zero. The sought area must be equal to: $$ S = p_1^{s_1} \cdot p_2^{s_2} \cdot p_3^{s_3} \ldots p_k^{s_k}, $$ where $k$ is the number of lines in the answer. The lines must be sorted in increasing order of prime numbers $p_i$. Recall that a number $X$ is considered prime if it has exactly two positive integer divisors: $1$ and $X$. If the required area is equal to 1, then output two units: $\texttt{}$.

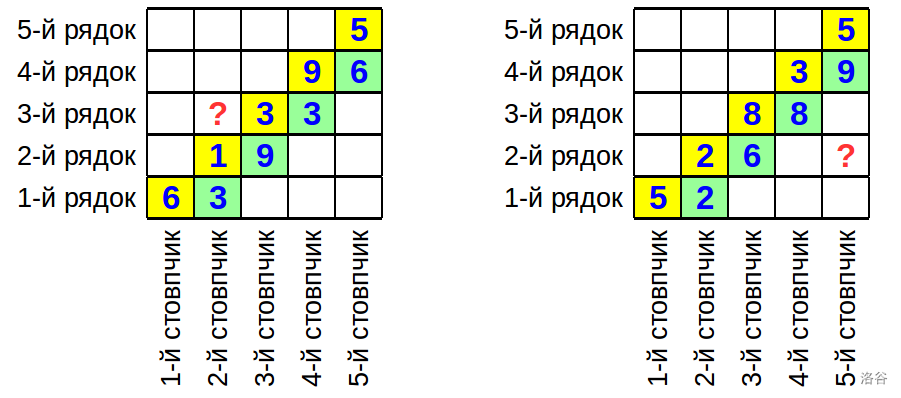
The area on the left in the figure corresponds to the first test from the condition. The area of the plot at the intersection of the 2nd column and the 3rd row is equal to: $$ S = 3^{-1} = \frac{1}{3} $$ The area on the right in the figure corresponds to the second test from the condition. The area of the plot at the intersection of the 5th column and the 2nd row is equal to: $$ S = 2^{1} \cdot 3^2 = 18 $$ ### Scoring - ($5$ points): Areas of all known areas --- prime numbers up to $100$ or one. The area, the area of which must be calculated, is located on the main or side diagonal. ($p - 1 = q$ or $p = q$) - ($5$ points): Areas of all known areas --- prime numbers up to $100$ or one. The area whose area needs to be calculated is located at the intersection of the $i$th column and the $(i+1)$th row. ($p + 1 = q$) - ($5$ points): The areas of all known plots do not exceed $10\,000$. The area, the area of which must be calculated, is located on the main or side diagonal. ($p - 1 = q$ or $p = q$) - ($5$ points): General restrictions on the area of all known plots. The area, the area of which must be calculated, is located on the main or side diagonal. ($p - 1 = q$ or $p = q$) - ($5$ points): The areas of all known plots do not exceed $10\,000$. The area whose area needs to be calculated is located at the intersection of the $i$th column and the $(i+1)$th row. ($p + 1 = q$) - ($5$ points): General restrictions on the area of all known plots. The area whose area needs to be calculated is located at the intersection of the $i$th column and the $(i+1)$th row. ($p + 1 = q$) - ($5$ points): The number of plots is $25$ ($n = 5$). The areas of all known plots do not exceed $100$. - ($5$ points): Areas of all known areas --- prime numbers up to $100$ or one. The area whose area needs to be calculated is in the upper left corner. ($p=1$, $q=n$) - ($5$ points): Areas of all known areas --- prime numbers up to $100$ or one. The area whose area needs to be calculated is in the lower right corner. ($p=n$, $q=1$) - ($5$ points): Areas of all known areas --- prime numbers up to $100$ or one. The area, the area of which must be calculated, is located above the main diagonal. ($p < q$) - ($5$ points): Areas of all known areas --- prime numbers up to $100$ or one. The area, the area of which must be calculated, is located under the main diagonal. ($p > q$) - ($5$ points): The areas of all known plots do not exceed $100$. The area whose area needs to be calculated is in the upper left corner. ($p=1$, $q=n$) - ($5$ points): The areas of all known plots do not exceed $100$. The area whose area needs to be calculated is in the lower right corner. ($p=n$, $q=1$) - ($5$ points): The areas of all known plots do not exceed $100$. The area, the area of which must be calculated, is located above the main diagonal. ($p < q$) - ($5$ points): The areas of all known plots do not exceed $100$. The area, the area of which must be calculated, is located under the main diagonal. ($p > q$) - ($5$ points): General restrictions on the area of all known plots. The area whose area needs to be calculated is in the upper left corner. ($p=1$, $q=n$) - ($5$ points): General restrictions on the area of all known plots. The area whose area needs to be calculated is in the lower right corner. ($p=n$, $q=1$) - ($8$ points): General restrictions on the area of all known plots. The area, the area of which must be calculated, is located above the main diagonal. ($p < q$) - ($7$ points): General restrictions on the area of all known plots. The area, the area of which must be calculated, is located under the main diagonal. ($p > q$)