P15084 [ICPC 2024 Chengdu R] Two Convex Holes

考虑三维笛卡尔坐标系中的两个不透明平面 $z = z_1$ 和 $z = z_2$（$z_1 < z_2$）。每个平面上都有一个凸多边形孔洞，分别记为 $P_1$ 和 $P_2$，允许光线通过。 有一个点光源 $L$ 在平面 $z = z_0$（$z_2 < z_0$）上沿平行于 $xOy$ 平面的方向移动。光源在时刻 $t = 0$ 从初始位置 $(x_0, y_0, z_0)$ 出发，以恒定速度 $\boldsymbol{v} = (v_x, v_y, 0)$ 运动。因此，在任意时刻 $t$，光源的位置为 $(x_0 + v_x t, y_0 + v_y t, z_0)$。 对于平面 $z = 0$ 上的一个点 $A$，定义它在时刻 $t$ 被**照亮**，当且仅当线段 $LA$ 与两个多边形 $P_1$ 和 $P_2$ 的内部（包括边界）均相交。时刻 $t$ 的**照亮面积**，记为 $f(t)$，是平面 $z = 0$ 上所有被照亮点形成的面积。 定义在时间段 $[t_1, t_2]$ 上的**平均照亮面积**，记为 $\mathbb{E}[f(t) | t \sim U(t_1,t_2)]$，为 $f(t)$ 在区间 $[t_1, t_2]$ 上的期望值，其中 $t$ 假设为 $[t_1, t_2]$ 上均匀分布的随机变量。 给定多个时间段 $[t_1, t_2]$，你的任务是找出每个时间段内的平均照亮面积。

- 第一行包含一个整数 $T$（$1\le T\le 10^4$），表示测试用例的数量。 - 对于每个测试用例： - 第一行包含五个整数 $x_0$、$y_0$、$z_0$、$v_x$、$v_y$（$-10^5 \le x_0, y_0 \le 10^5$，$1 \le z_0 \le 10^5$，$-10^3 \le v_x, v_y \le 10^3$），分别表示光源的初始位置 $(x_0, y_0, z_0)$ 及其速度向量 $\boldsymbol{v} = (v_x, v_y, 0)$。保证 $\boldsymbol{v} \neq (0, 0, 0)$。 - 第二行包含两个整数 $n_1$ 和 $z_1$（$3 \le n_1 \le 10^5$，$1 \le z_1 \le 10^5$），分别表示多边形 $P_1$ 的顶点数和 $z_1$ 的值。接下来的 $n_1$ 行每行包含两个整数 $x_i$ 和 $y_i$（$-10^5 \le x_i, y_i \le 10^5$），按逆时针顺序描述 $P_1$ 的顶点。 - 接下来一行包含两个整数 $n_2$ 和 $z_2$（$3 \le n_2 \le 10^5$，$1 \le z_2 \le 10^5$），分别表示多边形 $P_2$ 的顶点数和 $z_2$ 的值。接下来的 $n_2$ 行每行包含两个整数 $x_j$ 和 $y_j$（$-10^5 \le x_j, y_j \le 10^5$），按逆时针顺序描述多边形 $P_2$ 的顶点。 - 保证 $P_1$ 和 $P_2$ 均无三点或更多点共线。 - 接下来一行包含一个整数 $q$（$1 \le q \le 10^5$），表示查询的数量。接下来的 $q$ 行每行包含两个整数 $t_1$ 和 $t_2$（$0 \le t_1 \le t_2 \le 10^3$），表示一个时间段。 - 保证所有测试用例的 $n_1+n_2$ 之和以及 $q$ 之和分别不超过 $10^5$，且 $z_1 < z_2 < z_0$。

对于每个查询，输出一个实数表示平均照亮面积。只有当你的答案与正确答案的相对误差或绝对误差不超过 $10^{-4}$ 时，才被视为正确。

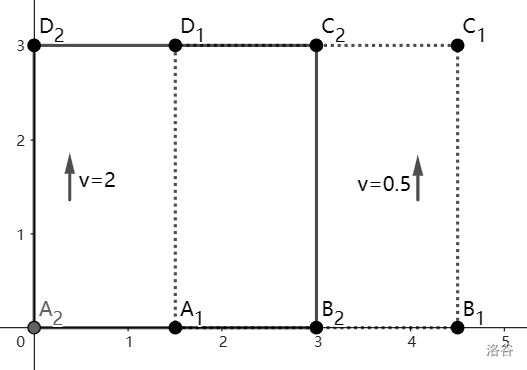
对于此示例，凸多边形 $P_1$ 和 $P_2$ 在 $t=0$ 时刻在 $xOy$ 平面上的投影，以及这些投影的运动，如下图所示。多边形 $A_1B_1C_1D_1$ 是多边形 $P_1$ 的投影，多边形 $A_2B_2C_2D_2$ 是多边形 $P_2$ 的投影。 :::align{center}  ::: 翻译由 DeepSeek V3 完成