P15087 [UOI 2025 II Stage] Area of the Cake

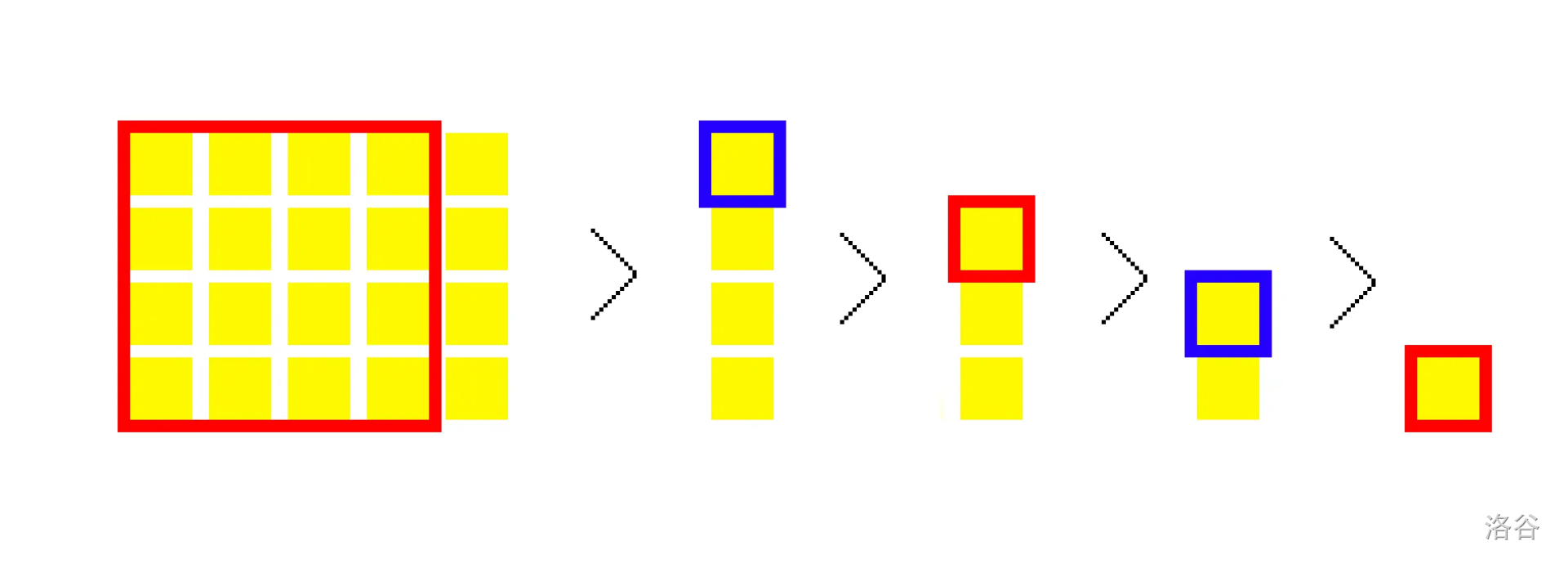
哥萨克人 Vus 和哥萨克人 Us 正在一块尺寸为 $n \times m$ 的矩形蛋糕上玩游戏。 他们轮流行动（Vus 先手），从蛋糕上切下一个尽可能大的正方形块，使得该正方形的四条边中有三条在回合开始时与蛋糕的边重合。然后，该玩家拿走这块蛋糕。如果蛋糕本身就是正方形，则该玩家拿走剩下的整块蛋糕。 :::align{center}  切割 $4 \times 5$ 的蛋糕。红色边框的蛋糕块由 Vus 切下，蓝色边框的由 Us 切下。 ::: 当整块蛋糕被成功分割后，Vus 拿走的正方形面积总和为 $p$，Us 拿走的为 $q$。 哥萨克们玩得太投入，以至于忘记了蛋糕的尺寸，于是他们向你求助。请找出任意可能的初始蛋糕尺寸。

第一行包含两个整数 $p$ 和 $q$（$0\leq p,q\leq10^{12}; p+q>0$）。

输出两个整数 $n$ 和 $m$ ——初始蛋糕的尺寸。如果有多个正确答案，输出任意一对即可。 如果这样的蛋糕不存在，输出 $-1$。

第一个示例的示意图已在题目描述中给出。 在第二个示例中，一块 $2\times 2$ 的蛋糕满足条件，因为 Vus 会在他的第一步拿走面积为 $4$ 的整块蛋糕。 翻译由 DeepSeek V3 完成