P15092 [UOI 2025 II Stage] Diagonal Numbers

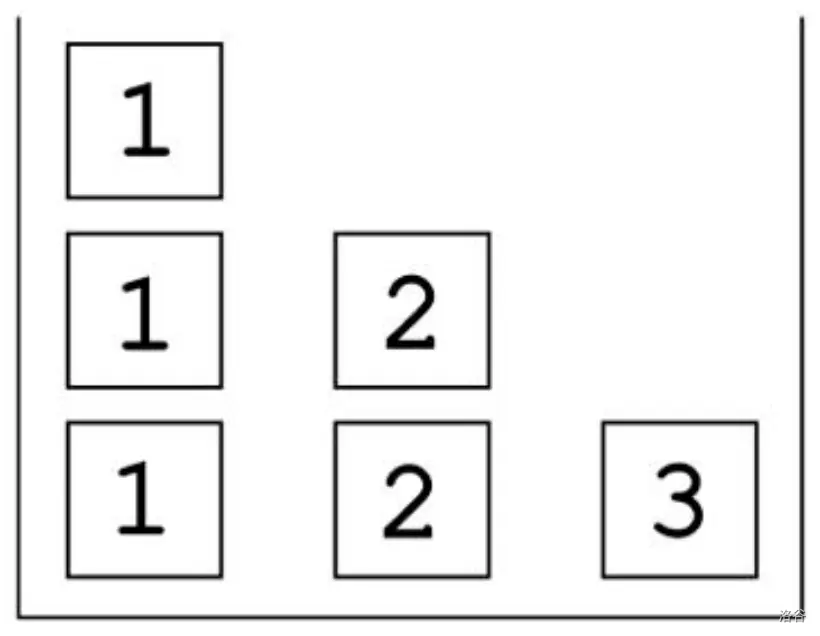
Vasylko 得到了写有数字 $1$ 到 $n$ 的方块。其中写有数字 $n$ 的方块有 $1$ 个，写有数字 $n-1$ 的方块有 $2$ 个，依此类推，写有数字 $2$ 的方块有 $n-1$ 个，写有数字 $1$ 的方块有 $n$ 个。 他将这些方块摆放在一个没有上边框的正方形框架内，使得所有方块都位于从左上角到右下角的对角线下方。最左边的第一列有 $n$ 个写有数字 $1$ 的方块；第二列有 $n-1$ 个写有数字 $2$ 的方块……第 $n$ 列有 $1$ 个写有数字 $n$ 的方块。也就是说，第 $i$ 列有 $n-i+1$ 个写有数字 $i$ 的方块。 :::align{center}  初始状态 ::: Vasylko 想重新排列它们，使得所有方块都位于**另一条对角线**下方。这样，从下往上数的第一行应有 $n$ 个写有数字 $1$ 的方块；第二行应有 $n-1$ 个写有数字 $2$ 的方块……第 $n$ 行应有 $1$ 个写有数字 $n$ 的方块。也就是说，第 $i$ 行应有 $n-i+1$ 个写有数字 $i$ 的方块。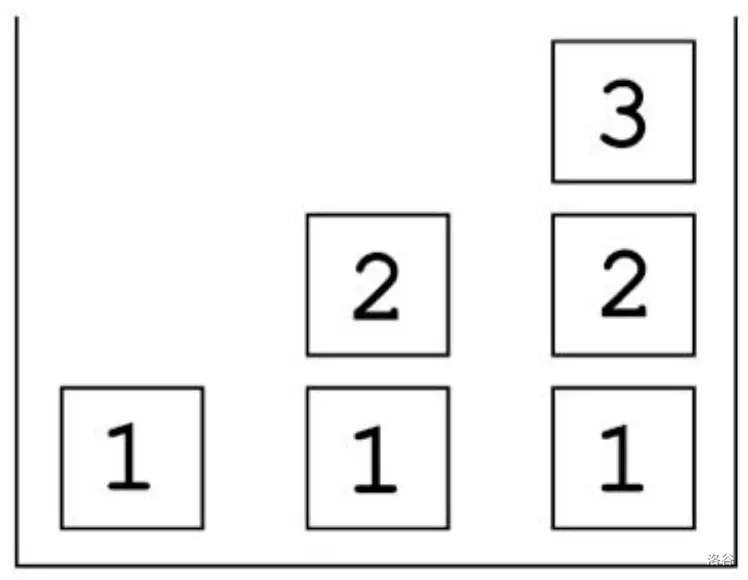 :::align{center}  最终状态 ::: 他还决定，只将方块从一列的顶部移动到另一列的顶部（不一定是相邻列）。请以最高效的方式帮助他——找出他所需的最少移动次数，并输出 Vasylko 应进行的移动。 **你可以获得部分分数；详见下文。**

第一行包含一个整数 $n$（$3 \le n \le 1000$）——正方形的尺寸。

- 第一行输出一个整数 $k$（$1 \leq k \leq 10^6$）——重新排列方块所需的最少移动次数。 - 接下来的 $k$ 行，每行输出两个整数 $a$ 和 $b$（$1 \leq a, b \leq n$；$a \neq b$），其中 $a$ 表示取出方块的列号，$b$ 表示放入方块的列号。

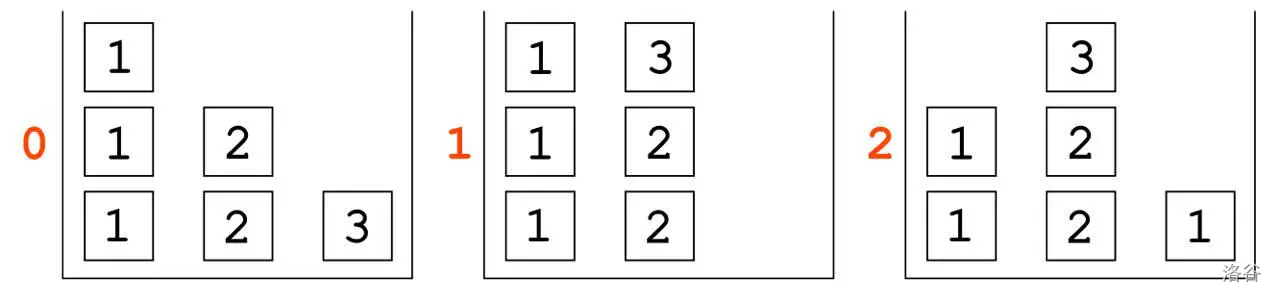
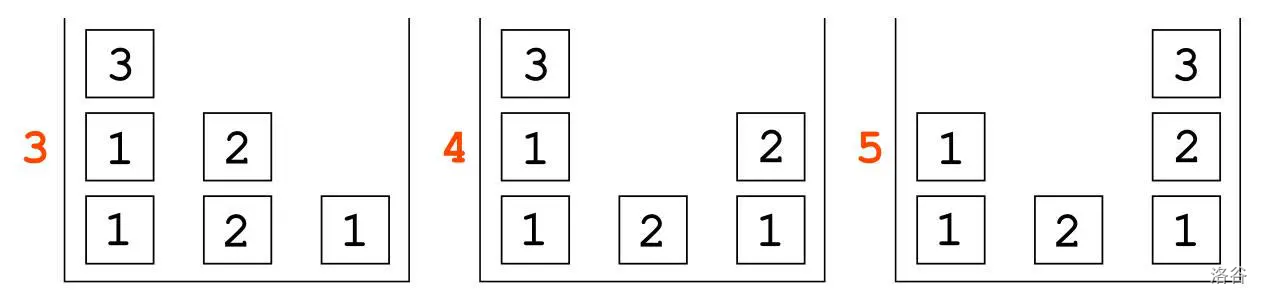
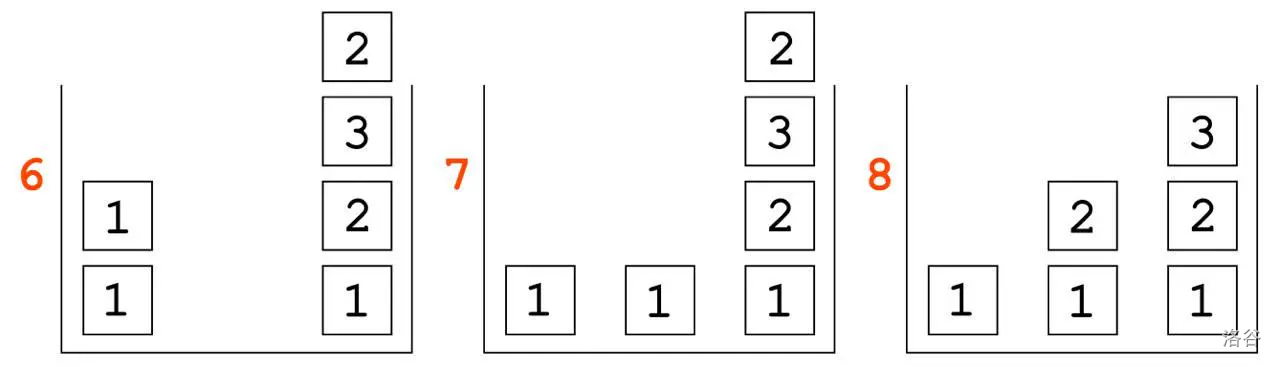
首先，我们将处理最后一列。因此，以最少移动次数重新排列方块的唯一第一步可能是将 $3$ 从第三列移动到第二列，因为如果不移动 $3$ 或不将其移动到第二列，我们将无法将 $1$ 放在第三列的开头。 :::align{center}  前 3 个状态 ::: 放置好 $1$ 之后，我们需要将 $2$ 和 $3$ 放到它们在第三列的正确位置。同样，唯一的方法是先将 $3$ 移动到第一列，否则我们将无法在下一步中将 $2$ 放入第三列，然后再将 $3$ 放回它的位置。 :::align{center}  接下来 3 个状态 ::: 此后，我们想要正确放置第二列。为了让 $1$ 成为第一个数字，我们首先需要取出 $2$，而 $2$ 只能在最后一列被取出。放置好 $1$ 后，我们只需将 $2$ 放回第二列，即可达到期望的方块状态。 :::align{center}  最后 3 个状态 ::: ### 评分细则 - （$12$ 分）：$n = 4$； - （$20$ 分）：$n = 5$； - （$20$ 分）：$n = 6$； - （$20$ 分）：$n \le 10$； - （$20$ 分）：$n \le 100$； - （$8$ 分）：无额外限制。 对于每个测试组，如果你为该组中每个测试输出了正确的 $k$，你可以获得该组一半的分数。如果你输出了错误的 $k$ 但移动指令正确，你也可以获得四分之一的分数；此时要求 $k \le 10^6$。 注意，要获得一半的分数，你需要输出正确的 $k$ 并且： - 要么不输出其他内容，即只输出 $k$，不输出移动指令； - 要么完整输出所有 $k$ 条移动指令，其中所有列号都在 $1$ 到 $n$ 之间。除此之外没有其他要求。 如果你只输出部分指令、或输出过多指令、或输出的数字不是列号等，你将获得 $0$ 分。 翻译由 DeepSeek V3 完成