P15099 [ICPC 2025 LAC] Exciting Business Opportunities

Treeland 的地铁系统由 $N$ 个车站组成，这些车站通过 $N-1$ 条双向隧道连接。隧道的布局保证任意两个车站之间总是可以通行。该系统已经被认为是该国最高效的地铁系统：系统中的每对车站之间都有列车运行。 地铁改进部门的 Alejandro 接到一项任务，要使该系统对乘客和商业更加友好、更具吸引力。为此，该部门收集了来自公司的 $P$ 份提案。每份提案要么是赞助某个车站（基本上就是在车站上添加带有公司名称的标识），要么是在某个车站开设一家企业（例如餐厅、商店等）。请注意，每个车站可以接受的提案数量没有限制。 然而，愿意在该系统中开设企业的公司表示，除非他们企业所在的车站 $X$ 是一个被赞助的车站，或者存在一条连接两个被赞助车站的列车线路经过 $X$，否则他们将撤回提案。当然，Alejandro 不希望选择那些之后会被撤回的提案。因此，他将确保选择一个提案集合，使得集合中的任何提案都不会被撤回。他称这样的集合为 **有效的提案集合**。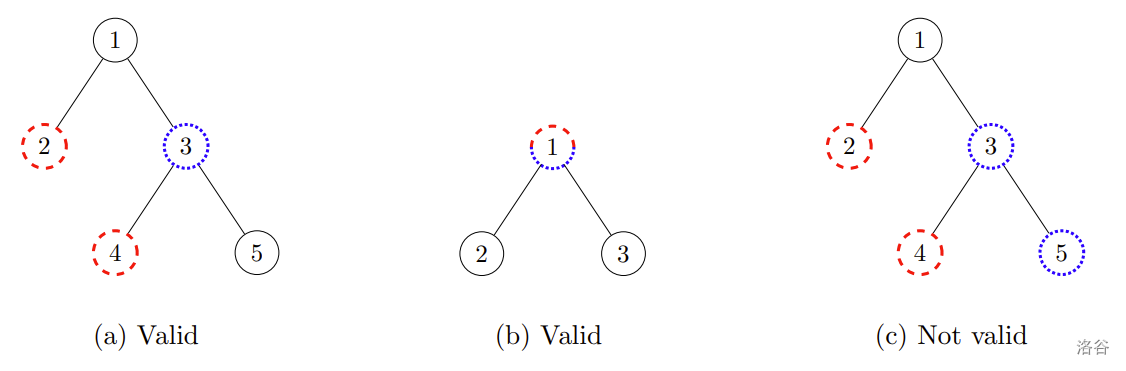 下图展示了被赞助的车站用红色/虚线圆圈表示，企业用蓝色/点状圆圈表示。图 (a) 中的提案集合是有效的，因为车站 3 的企业提案恰好位于两个被赞助车站 2 和 4 之间的路径上。图 (b) 中的提案集合也是有效的，因为车站 1 的企业提案恰好位于一个被赞助车站上。相反，图 (c) 中的提案集合是无效的：尽管车站 3 的企业提案位于两个被赞助车站之间的路径上，但车站 5 的企业提案并不满足条件。 :::align{center}  ::: 为了选择一个有效的集合，Alejandro 拿到了这 $P$ 份提案（每份提案都写在一张纸上），并将它们从 $1$ 到 $P$ 编号。现在他想选择一个连续的提案区间，使其构成一个有效的集合。更准确地说，他想选择两个整数 $i$ 和 $j$，满足 $1 \le i \le j \le P$，使得提案 $i, i+1, \dots, j$ 构成一个有效的集合；此外，他希望这个集合尽可能大。Alejandro 不确定他应选择的区间起始提案 $i$ 是哪一个。请帮助他计算，对于每个从 $1$ 到 $P$ 的 $i$，以提案 $i$ 为起始的、构成有效集合的最大连续提案区间的大小。

第一行包含一个整数 $N$（$2 \le N \le 10^5$），表示地铁系统中的车站数量。每个车站由 $1$ 到 $N$ 之间的一个不同整数标识。 接下来的 $N-1$ 行，每行包含两个整数 $U$ 和 $V$（$1 \le U, V \le N$ 且 $U \ne V$），表示车站 $U$ 和 $V$ 之间有一条双向隧道。保证使用这些隧道可以从任意车站到达其他任意车站。 接下来一行包含一个整数 $P$（$1 \le P \le 10^5$），表示公司提交的提案数量。每份提案由 $1$ 到 $P$ 之间的一个不同整数标识。 接下来的 $P$ 行中的第 $i$ 行描述提案 $i$，包含一个字符 $C$ 和一个整数 $X$（$1 \le X \le N$）。对于赞助提案，$C$ 是小写字母 “s”；对于企业提案，$C$ 是小写字母 “b”；在这两种情况下，$X$ 都是对应的车站。请注意，每个车站可以拥有任意数量的任意类型的提案。

输出 $P$ 行。第 $i$ 行必须包含一个整数，表示以提案 $i$ 为起始的、构成有效集合的最大连续提案区间的大小。

翻译由 DeepSeek V3 完成