P15100 [ICPC 2025 LAC] Festival Signs

在一个节日期间，广告牌会在不同时刻被添加到舞台上或从舞台上移除。每个广告牌呈矩形，垂直于地面放置，其中一条边稳固地接触地面。 一个网络摄像头正在直播节日，展示舞台的二维图像。在这幅图像中，底部边界对应地面。每个广告牌覆盖图像中的一个矩形区域。一个广告牌由一个区间 $[A, B]$ 和一个高度 $H$ 描述，这意味着它覆盖图像中所有满足 $A \le x \le B$ 且 $0 \le y < H$ 的点 $(x, y)$。 请注意，广告牌覆盖矩形底部和侧边边界上的点，但不覆盖顶部边界上的点。此外，表示不同广告牌的矩形可以重叠。 在直播过程中，经理会在不同时刻进行多次查询。每次查询指定一个区间 $[L, R]$，并询问在满足 $L \le x \le R$ 的所有未被覆盖的点 $(x, y)$ 中，最小的 $y$ 值（其中 $x$ 和 $y$ 是实数）。 你的任务是编写一个程序来处理一系列 $N$ 个事件：广告牌的添加、广告牌的移除，以及关于给定区间内最小未被覆盖高度的查询。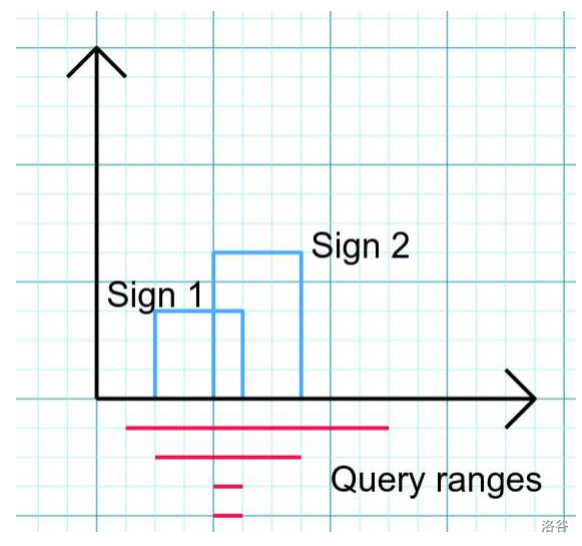 例如，考虑以下按时间顺序给出的 $N = 7$ 个事件序列（见下图）： - 添加一个广告牌，其 $[A, B] = [2, 5]$，$H = 3$。 - 添加一个广告牌，其 $[A, B] = [4, 7]$，$H = 5$。 - 进行查询 $[1, 10]$。该查询的答案是 $0$。该区间内具有最小高度的未被覆盖点的一个例子是坐标为 $(1.5, 0)$ 的点。 - 进行查询 $[2, 7]$，答案为 $3$。 - 进行查询 $[4, 5]$，答案为 $5$。 - 移除第二次添加的广告牌。 - 进行查询 $[4, 5]$，答案为 $3$。请注意，移除第二个广告牌改变了查询 $[4, 5]$ 的答案。 :::align{center}  :::

第一行包含一个整数 $N$（$1 \le N \le 2 \cdot 10^5$），表示事件的数量。 接下来的 $N$ 行按时间顺序描述每个事件。每行的内容取决于事件类型，如下所示： - **广告牌添加**：该行包含字符 “+”（加号）和三个整数 $A$、$B$ 和 $H$（$1 \le A, B, H \le 10^9$ 且 $A < B$），表示添加一个广告牌，其覆盖图像中的矩形区域，如题目描述中所述。每个添加的广告牌被分配一个从 $1$ 开始的连续整数标识符。 - **广告牌移除**：该行包含字符 “-”（减号）和一个整数 $I \ge 1$，表示移除标识符为 $I$ 的广告牌。保证 $I$ 标识一个已被添加且之前未被移除的广告牌。 - **查询**：该行包含字符 “?”（问号）和两个整数 $L$ 和 $R$（$1 \le L < R \le 10^9$），询问区间 $[L, R]$ 内最小未被覆盖高度，如题目描述中所述。保证输入中至少包含一个查询。

对每个查询输出一行，包含一个整数，表示对应区间内的最小未被覆盖高度。

翻译由 DeepSeek V3 完成