P15101 [ICPC 2025 LAC] Game of Pieces

If you’ve ever played Tetris for long enough, you might have experienced the **Tetris effect** – seeing falling blocks even after you have stopped playing. To stay focused on solving problems and avoid such distractions, we will consider a simplified version of the game. The game is played on a board composed of square cells arranged in a grid. Columns of the grid are numbered sequentially from left to right. The board is infinite to the right and to the top. Each cell is either empty or filled, and initially, all cells are empty. A sequence of $N$ rectangular pieces is given, and the pieces are dropped onto the board one at a time. Pieces have different sizes. A piece of size $L$ is either vertical ($L \times 1$ cells) or horizontal ($1 \times L$ cells). When a piece is dropped at a specified column, it starts at a location above all the currently filled cells and falls straight down until it either reaches the bottom of the board or lands on top of an already filled cell. Once a piece lands, it fills its final set of cells. Each time a piece lands, the game is considered **safe** if no empty cell has a filled cell above it; otherwise the game is **unsafe**, the offending piece is removed from the board, and the game continues with the next piece as if it had never been dropped. In the example below, corresponding to the first sample input, the game becomes unsafe once the second piece lands, hence the piece is removed and the next pieces keep the game safe. 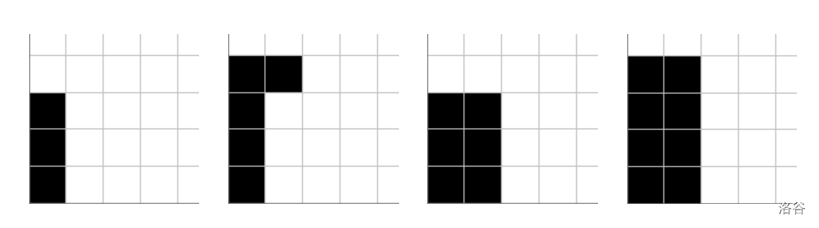:::align{center}  ::: Given the sequence of pieces and their drop positions, your task is to determine, for each piece, whether it makes the board unsafe after landing.

The first line contains an integer $N$ ($1 \le N \le 2 \cdot 10^5$), indicating the number of pieces. Each of the next $N$ lines describes a piece with a character $C$ and two integers $L$ and $P$ ($1 \le L \le 10^9$ and $1 \le P \le 10^{18}$), representing respectively the type of the piece, its length, and the position where it is dropped. For a vertical piece, $C$ is the character “|” (pipe), the piece has $L \times 1$ cells, and it is dropped at column $P$. For a horizontal piece, $C$ is the character “-” (hyphen), the piece has $1 \times L$ cells, and it is dropped spanning columns $P, P+1, \dots, P+L-1$.

Output a single line with a string of length $N$. The $i$-th character of the string must be the uppercase letter “U” if the game becomes unsafe immediately after the $i$-th piece lands on the board, and the uppercase letter “S” otherwise.