P15139 [SWERC 2025] Expansion Plan 2

You are dealing with side quests in the video game Expansion Plan 2. There is an infinite grid of **bonus levels**, with coordinates $(x, y)$ (specifically, the cell immediately above $(0,0)$ is $(0,1)$, and the cell immediately on the right of $(0,0)$ is $(1,0)$). Initially, only the bonus level at $(0,0)$ is **unlocked**. Given a string $a_1a_2 \dots a_l$ of length $l$ consisting of characters "4" and "8", you play $l$ times in a row; at the $i$-th play you obtain a **score** equal to $s_i \in \{"4", "8"\}$. For each $i$ from 1 to $l$: - if $s_i = \text{"4"}$: for each bonus level, if it is orthogonally adjacent (i.e., it shares a side) to a level which was already **unlocked** before the $i$-th play, it becomes unlocked; otherwise, its state remains the same; - if $s_i = \text{"8"}$: for each bonus level, if it is orthogonally or diagonally adjacent (i.e., it shares a side or a corner) to a level which was already **unlocked** before the $i$-th play, it becomes unlocked; otherwise, its state remains the same. You are given a string $s$ of length $n$ consisting of characters "4" and "8". You have to answer $q$ queries. In each query, you start with an infinite grid where only the bonus level $(0,0)$ is unlocked, and you are given four integers $l, r, x, y$. You have to determine whether the bonus level $(x,y)$ is unlocked after getting the scores in the substring $[l, r]$ of $s$.

The first line contains two integers $n, q$ ($1 \le n, q \le 2 \cdot 10^5$) — the length of the string and the number of queries, respectively. The second line contains a string $s$ of length $n$ consisting of characters "4" and "8". Each of the next $q$ lines contains four integers $l, r, x, y$ ($1 \le l \le r \le n$, $-10^9 \le x, y \le 10^9$), representing a query on the substring $[l, r]$ and the bonus level $(x, y)$.

For each query, output **YES** if the bonus level $(x, y)$ is **unlocked** after getting the scores in the substring $[l, r]$ of $s$, and **NO** otherwise. The judge is case-insensitive (for example, YES, Yes, yes, yEs will all be recognized as positive answers).

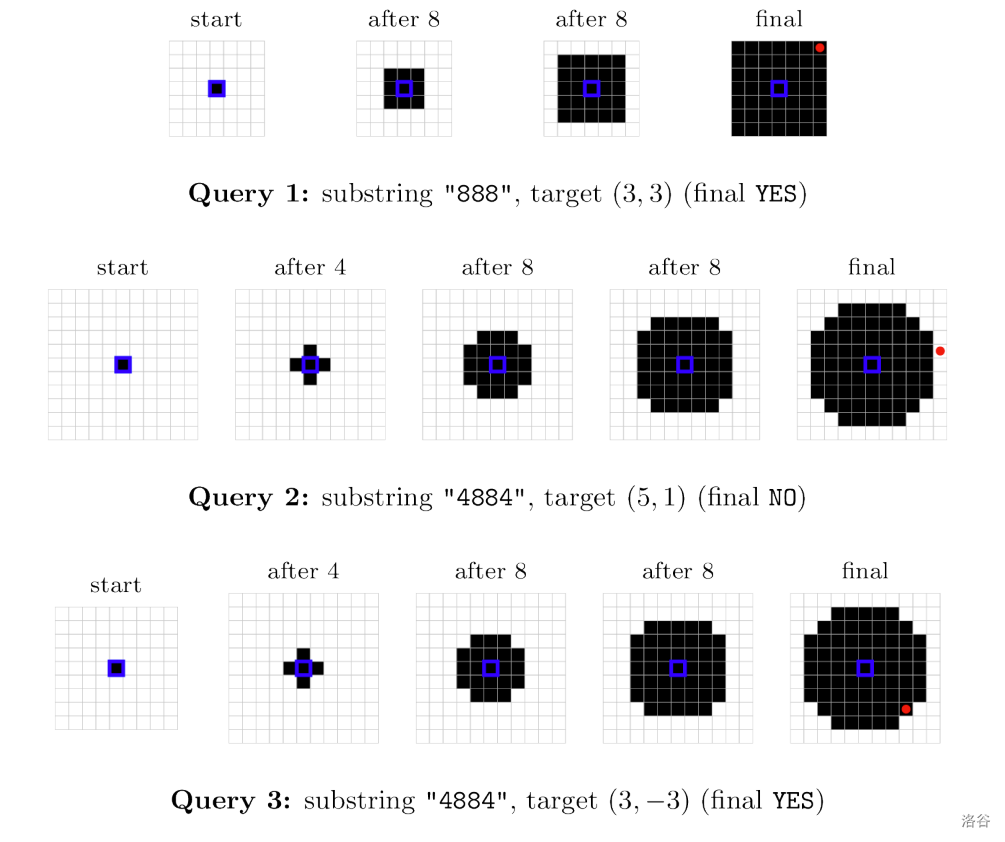
#### Explanation of sample 1. The first three queries are illustrated below: :::align{center}  ::: In the first query, $[l, r] = [8, 10]$, and $(x, y) = (3, 3)$. The substring $[8, 10]$ of $s$ is "888". After getting the scores in this substring, the bonus level $(3, 3)$ is unlocked, so the answer is YES. In the second query, the bonus level $(5, 1)$ is not unlocked after getting the scores in the substring "4884".