P15139 [SWERC 2025] Expansion Plan 2

你正在处理电子游戏 **扩张计划 2** 中的支线任务。 有一个无限的**奖励关卡**网格，坐标为 $(x, y)$（具体来说，$(0,0)$ 正上方的格子是 $(0,1)$，$(0,0)$ 正右方的格子是 $(1,0)$）。初始时，只有位于 $(0,0)$ 的奖励关卡处于**解锁**状态。 给定一个长度为 $l$、由字符“4”和“8”组成的字符串 $a_1a_2 \dots a_l$，你连续进行 $l$ 次游戏；在第 $i$ 次游戏中，你获得一个**分数** $s_i \in \{"4", "8"\}$。对于每个 $i$ 从 $1$ 到 $l$： - 如果 $s_i = \text{"4"}$：对于每个奖励关卡，如果它在第 $i$ 次游戏之前与一个已经**解锁**的关卡**正交相邻**（即共享一条边），则该关卡变为解锁；否则，其状态保持不变； - 如果 $s_i = \text{"8"}$：对于每个奖励关卡，如果它在第 $i$ 次游戏之前与一个已经**解锁**的关卡**正交或对角相邻**（即共享一条边或一个角），则该关卡变为解锁；否则，其状态保持不变。 给定一个长度为 $n$、由字符“4”和“8”组成的字符串 $s$。 你需要回答 $q$ 个查询。在每个查询中，你从一个只有奖励关卡 $(0,0)$ 解锁的无限网格开始，并给定四个整数 $l, r, x, y$。你需要判断在获得 $s$ 的子串 $[l, r]$ 中的分数后，奖励关卡 $(x,y)$ 是否被解锁。

第一行包含两个整数 $n, q$（$1 \le n, q \le 2 \cdot 10^5$）—— 分别表示字符串的长度和查询的数量。 第二行包含一个长度为 $n$、由字符“4”和“8”组成的字符串 $s$。 接下来的 $q$ 行，每行包含四个整数 $l, r, x, y$（$1 \le l \le r \le n$，$-10^9 \le x, y \le 10^9$），表示对子串 $[l, r]$ 和奖励关卡 $(x, y)$ 的查询。

对于每个查询，如果奖励关卡 $(x, y)$ 在获得 $s$ 的子串 $[l, r]$ 中的分数后**解锁**，则输出 **YES**，否则输出 **NO**。 评测系统对大小写不敏感（例如，YES、Yes、yes、yEs 都会被识别为肯定答案）。

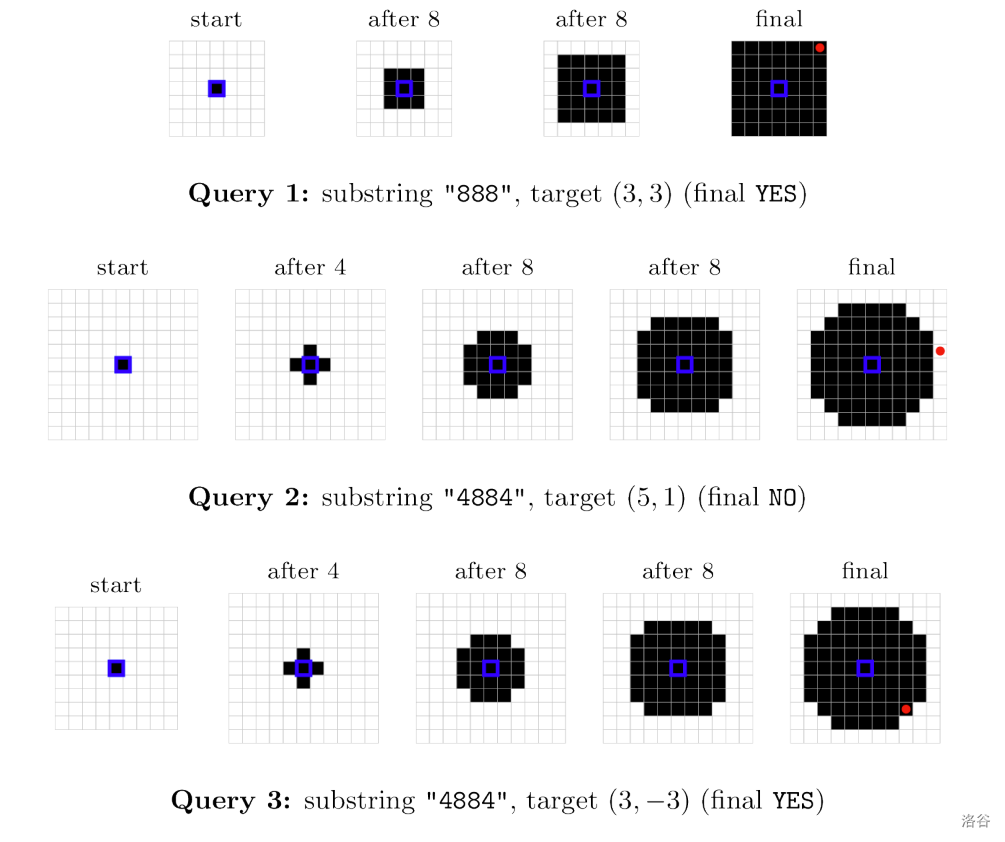
#### 样例解释 前三个查询的示意图如下： :::align{center}  ::: 在第一个查询中，$[l, r] = [8, 10]$，且 $(x, y) = (3, 3)$。$s$ 的子串 $[8, 10]$ 是“888”。在获得该子串中的分数后，奖励关卡 $(3, 3)$ 被解锁，因此答案为 YES。 在第二个查询中，奖励关卡 $(5, 1)$ 在获得子串“4884”中的分数后并未解锁。 翻译由 DeepSeek 完成