P15140 [SWERC 2025] Factory Table

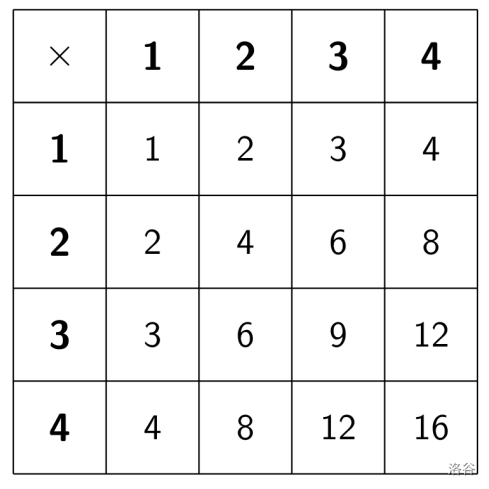
:::align{center}  ::: 你正在玩沙盒游戏 Mathcraft。每个等级为 $k$ 的制作台可以生成所有可能的乘积，这些乘积由 $1$ 到 $k$ 之间的两个数相乘得到。 如果你展开第 $k$ 个制作台，你会得到数组 $[1 \cdot 1, 1 \cdot 2, \dots, 1 \cdot k, 2 \cdot 1, 2 \cdot 2, \dots, 2 \cdot k, \dots, k \cdot 1, k \cdot 2, \dots, k \cdot k]$。例如，对于 $k = 4$，展开后的表是 $[1, 2, 3, 4, 2, 4, 6, 8, 3, 6, 9, 12, 4, 8, 12, 16]$。 你的朋友 Bob 制作了一个展开制作表的**连续**子数组。这个子数组是 $a_1, a_2, \dots, a_n$。 你想知道 Bob 有多熟练，因此你想找到他的制作台的最小可能等级。具体来说，你想确定最小的 $k$，使得 $a_1, a_2, \dots, a_n$ 作为子数组出现在第 $k$ 个展开表中。 数组 $b$ 是数组 $c$ 的子数组，当且仅当 $b$ 可以通过从 $c$ 的开头删除若干（可能为零或全部）元素，并从末尾删除若干（可能为零或全部）元素而得到。

每个测试包含多个测试用例。第一行包含测试用例的数量 $t$（$1 \le t \le 500$）。接下来是测试用例的描述。 每个测试用例的第一行包含一个整数 $n$（$2 \le n \le 100$）—— 数组 $a_1, a_2, \dots, a_n$ 的长度。 每个测试用例的第二行包含 $n$ 个整数 $a_1, a_2, \dots, a_n$（$1 \le a_i \le 10^9$）。 注意，所有测试用例的 $n$ 之和没有约束。

对于每个测试用例，输出一行一个整数：最小的制作台等级 $k$，使得数组 $a_1, a_2, \dots, a_n$ 作为连续子数组出现在第 $k$ 个展开表中。对于给定的输入，这样的 $k$ 总是存在。

#### 样例解释 在第一个测试用例中，数组 $[4, 6, 8, 10]$ 是第 $5$ 个展开表的子数组，该展开表为 $[1, 2, 3, 4, 5, 2, 4, 6, 8, 10, \dots, 5, 10, 15, 20, 25]$。没有更小的有效 $k$，因此答案为 $5$。 在第二个测试用例中，数组 $[8, 3, 6, 9, 12, 4]$ 是第 $4$ 个展开表的子数组，该展开表为 $[1, 2, 3, 4, 2, 4, 6, 8, 3, 6, 9, 12, 4, 8, 12, 16]$。 翻译由 DeepSeek 完成