P15151 [SWERC 2024] Building the Fort

你是一位罗马将军，正在设立防御堡垒对抗野蛮人。你只会建造直墙，因此你的堡垒将是多边形形状。 由于地形具有多个位于整数坐标处的山丘，你知道敌人的火炮只能以特定的方式安装，而且堡垒内较高的位置更容易受到攻击，这意味着： - 多边形的所有顶点必须具有在 $1$ 到 $10^9$（含）之间的整数坐标； - 已知的 $N$ 个点 $(x_i, y_i)$（$i = 1, \ldots, N$），其坐标在 $1$ 到 $10^9$ 之间（含），必须位于多边形的顶点中； - 任何整数坐标的点都不能严格位于多边形内部，否则该点将容易受到敌人火炮的攻击； - 多边形必须是**简单的**¹（显然，堡垒需要封闭，而且你不知道如何建造相交的墙）。 此外，由于建造这座堡垒的成本和有限的材料，你只能建造顶点数量小于或等于 $3N$ 的多边形。 可以证明，这样的多边形总是存在的。 ¹简单多边形是指由一条不自交、不重叠的封闭路径构成的多边形。

第一行包含整数 $N$。接下来的 $N$ 行每行包含两个空格分隔的整数 $x_i$、$y_i$，这些点必须位于多边形的顶点中。

第一行应输出 $K$，表示多边形的顶点数量。 接下来的 $K$ 行每行应输出两个空格分隔的整数 $x'_i$、$y'_i$，表示多边形顶点的坐标。它们必须按照构成一条封闭且不自交的路径的顺序输出，该路径定义了多边形的轮廓。 如果有多个解，你可以输出其中任意一个。

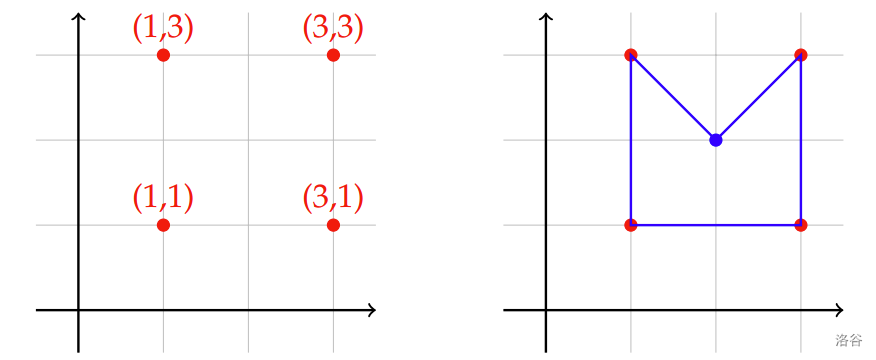
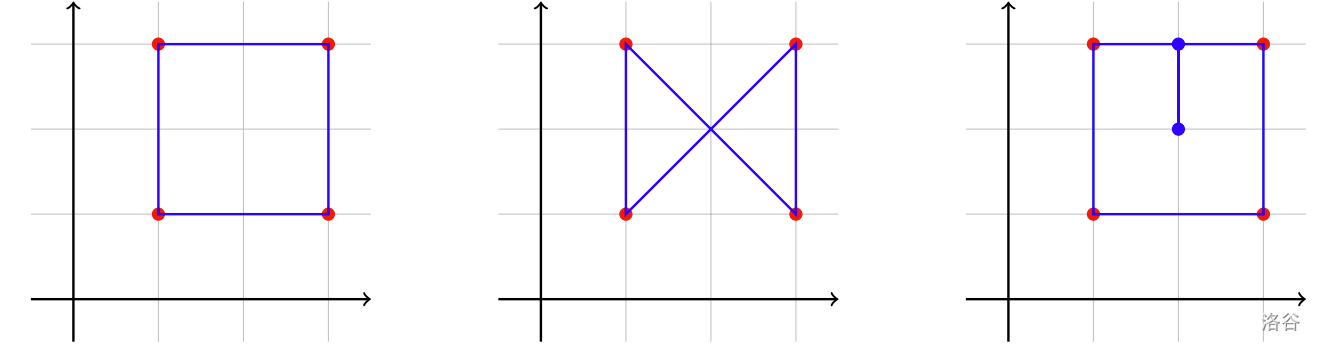
#### 样例解释 以下是样例输入的一个可能解： :::align{center}  ::: 另一方面，以下多边形不是有效的解： :::align{center}  ::: #### 数据范围 - $3 \leq N \leq 1000$； - 对于 $i = 1, \ldots, N$，$1 \leq x_i \leq 10^9$； - 对于 $i = 1, \ldots, N$，$1 \leq y_i \leq 10^9$； - 所有 $(x_i, y_i)$ 互不相同； - 对于 $i = 1, \ldots, K$，$1 \leq x'_i \leq 10^9$； - 对于 $i = 1, \ldots, K$，$1 \leq y'_i \leq 10^9$； - 所有 $(x'_i, y'_i)$ 必须互不相同。 翻译由 DeepSeek 完成