P15157 [SWERC 2024] Disk Covering

:::align{center}  ::: 在一片广阔平坦的绿色草地上，有几个来自古代的金色圆盘，形状为完美的圆形。根据传说，如果念诵咒语，圆盘覆盖的区域将变为火焰，以抵御敌人的攻击。当敌人到来时，你可以躲在一个被圆盘完全包围、但不在圆盘上的地方，从而被火焰与外界隔绝。 给定圆盘的位置和大小，判断这样的藏身之处是否存在。

第一行包含一个整数 $N$，表示圆盘的数量。接下来的 $N$ 行中，第 $i$ 行包含三个描述圆盘 $i$ 的整数：圆心的 x 坐标 $x_i$、y 坐标 $y_i$ 及其半径 $r_i$。

输出一个整数，如果存在这样的地方则输出 $1$，否则输出 $0$。

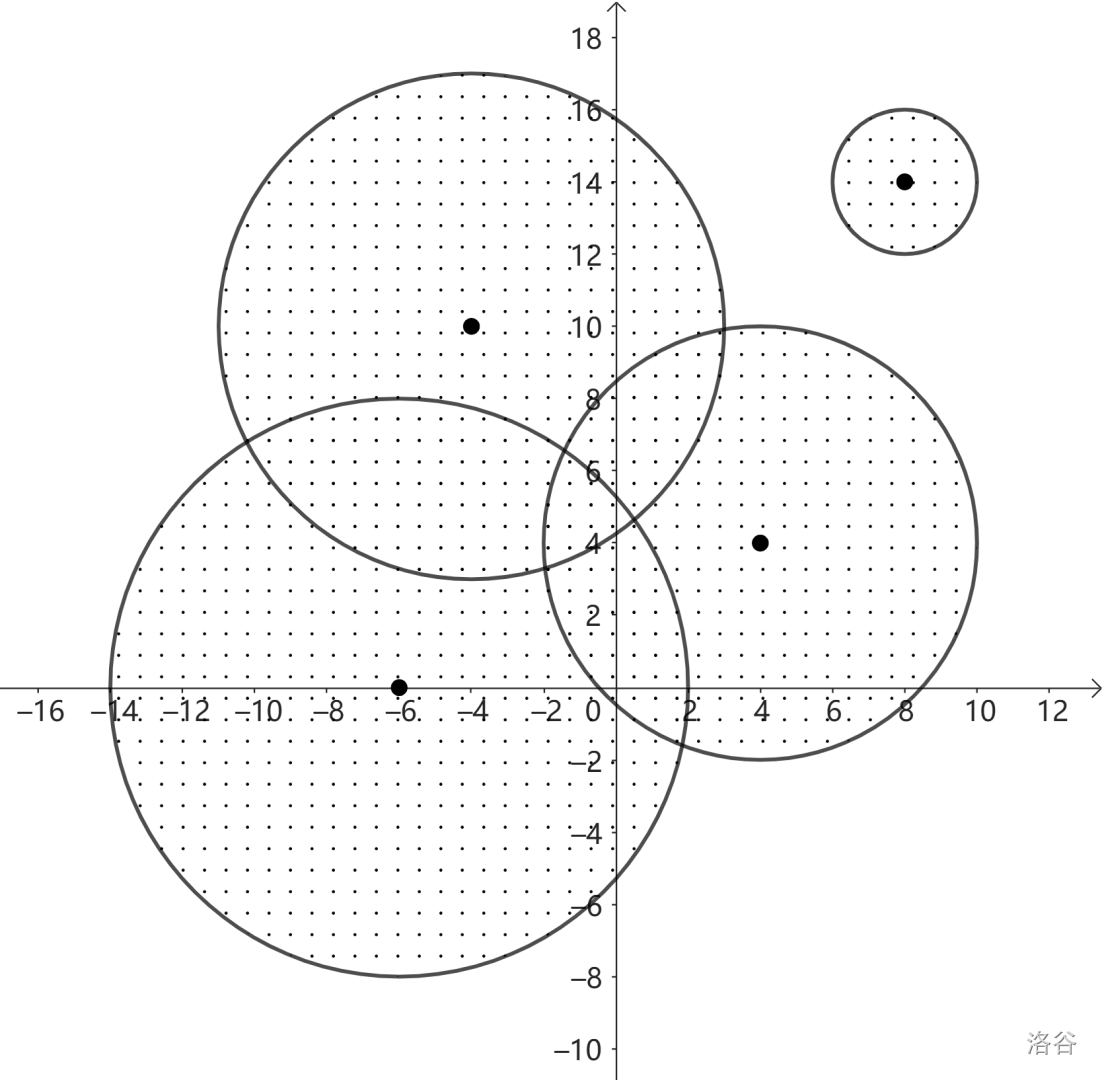
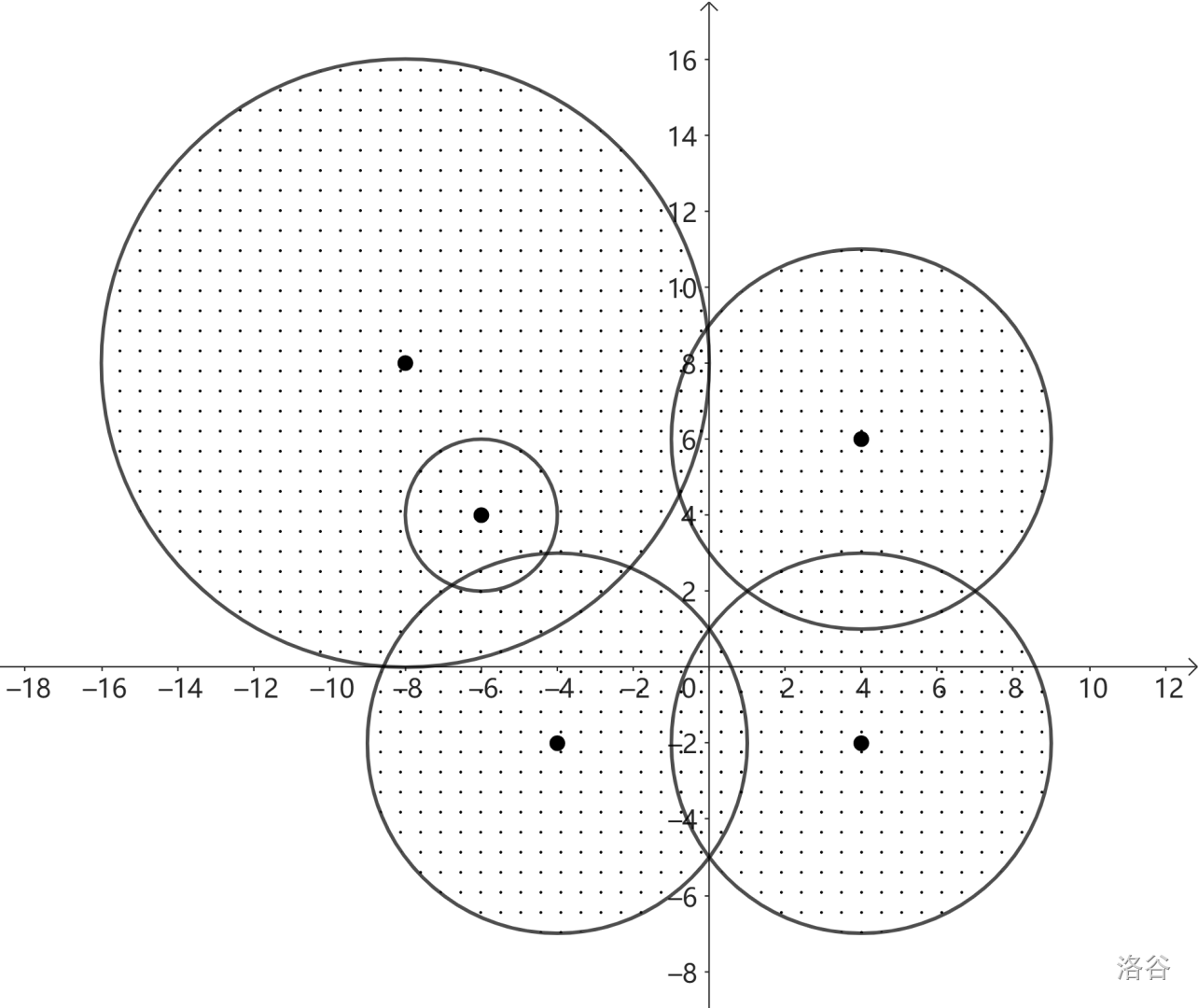
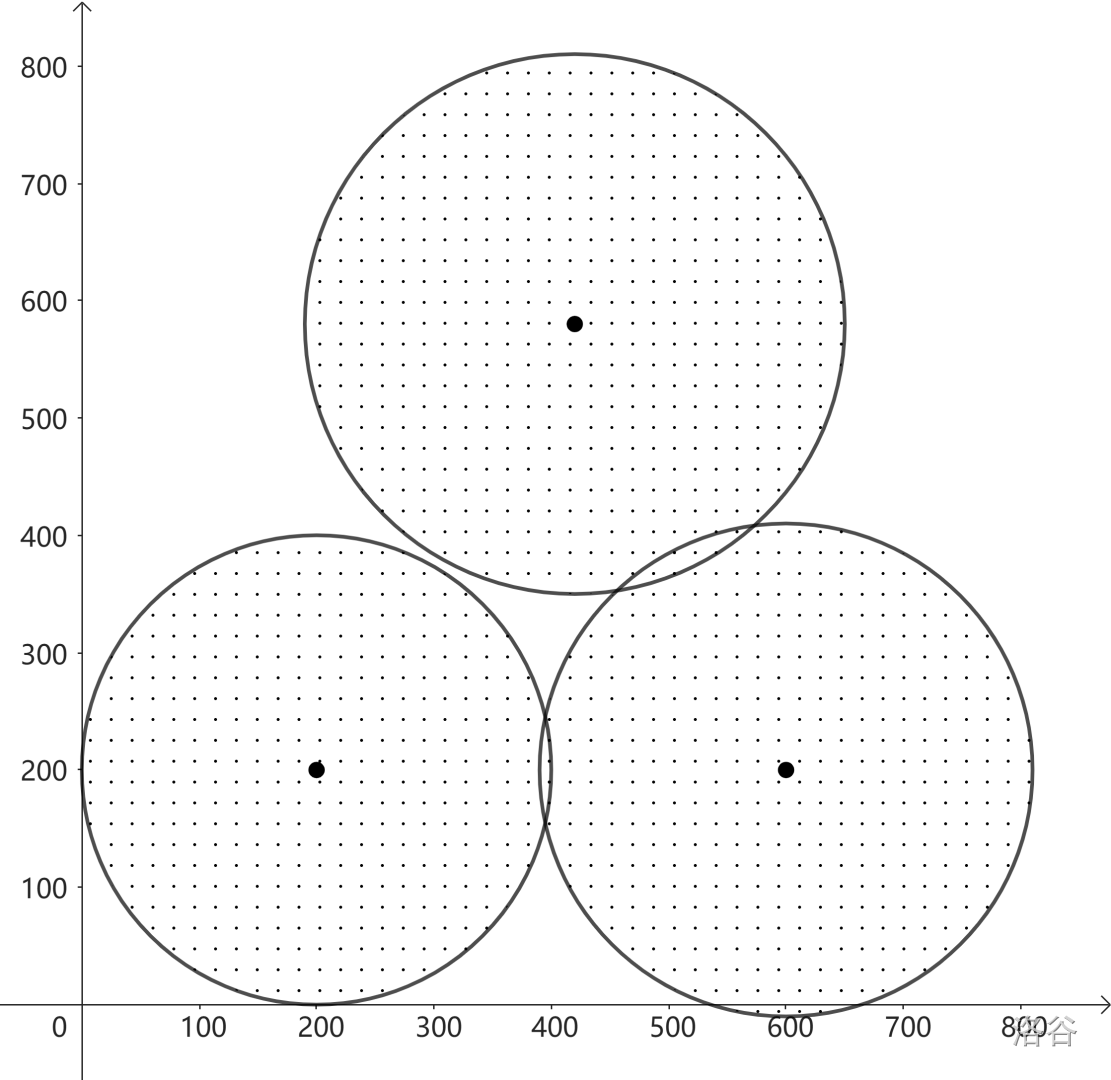
#### 样例解释 1 在此样例中，没有任何地方被圆盘完全包围且不在圆盘上。 :::align{center}  ::: #### 样例解释 2 在此样例中，点 $(-0.5, 3)$ 是我们可以藏身的地方之一。它被圆盘包围，但不在圆盘上。注意，虽然所有输入都是整数，但藏身点不一定必须是整数点。 :::align{center}  ::: #### 样例解释 3 在此样例中，没有任何地方被圆盘完全包围且不在圆盘上。 :::align{center}  ::: #### 数据范围 - $1 \leq N \leq 250$； - 对于所有 $i \leq N$，$-10^9 \leq x_i, y_i \leq 10^9$； - 对于所有 $i \leq N$，$1 \leq r_i \leq 10^9$； - 不存在三个圆盘的圆周相交于同一点； - 对于任意两个圆盘的圆周交点，任意两个交点之间的距离大于等于 $1$； - 不存在两个圆盘的圆周彼此相切（即恰好有一个交点）； - 对于圆周不相交的两个圆盘，一个圆盘圆周上的任意一点与另一个圆盘圆周上的任意一点之间的距离总是大于等于 $1$。 翻译由 DeepSeek 完成