P15160 [SWERC 2022] Walking Boy

One of the SWERC judges has a dog named Boy. Besides being a good competitive programmer, Boy loves fresh air, so she wants to be walked at least twice a day. Walking Boy requires $ 120 $ consecutive minutes. Two walks cannot overlap, but one can start as soon as the previous one has finished. :::align{center}  Boy before and after getting ACCEPTED on this problem. ::: Today, the judge sent $ n $ messages to the SWERC Discord server. The $ i $ -th message was sent $ a_i $ minutes after midnight. You know that, when walking Boy, the judge does not send any messages, but he can send a message right before or right after a walk. Is it possible that the judge walked Boy at least twice today? Note that a day has $ 1440 $ minutes, and a walk is considered to happen today if it starts at a minute $ s \ge 0 $ and ends right before a minute $ e \le 1440 $ . In that case, it must hold that $ e - s = 120 $ and, for every $ i = 1, \, 2 \, \dots, \, n $ , either $ a_i \le s $ or $ a_i \ge e $ .

Each test contains multiple test cases. The first line contains an integer $ t $ ( $ 1 \le t \le 100 $ ) — the number of test cases. The descriptions of the $ t $ test cases follow. The first line of each test case contains an integer $ n $ ( $ 1 \le n \le 100 $ ) — the number of messages sent by the judge. The second line of each test case contains $ n $ integers $ a_1, \, a_2, \, \dots, \, a_n $ ( $ 0 \le a_1 < a_2 < \cdots < a_n < 1440 $ ) — the times at which the messages have been sent (in minutes elapsed from midnight).

For each test case, output one line containing $ \texttt{YES} $ if it is possible that Boy has been walked at least twice, and $ \texttt{NO} $ otherwise.

In the **first test case**, the judge has sent a message at each time multiple of $100$ (excluding $0$). It is impossible that he has walked Boy even once. In the **second test case**, the times are the same as above, but $500$ and $1000$ are missing. The judge could have walked Boy, for instance, during the time intervals $[440, 560]$ and $[980, 1100]$. The situation is illustrated in the picture below, where the walks are represented by green intervals. 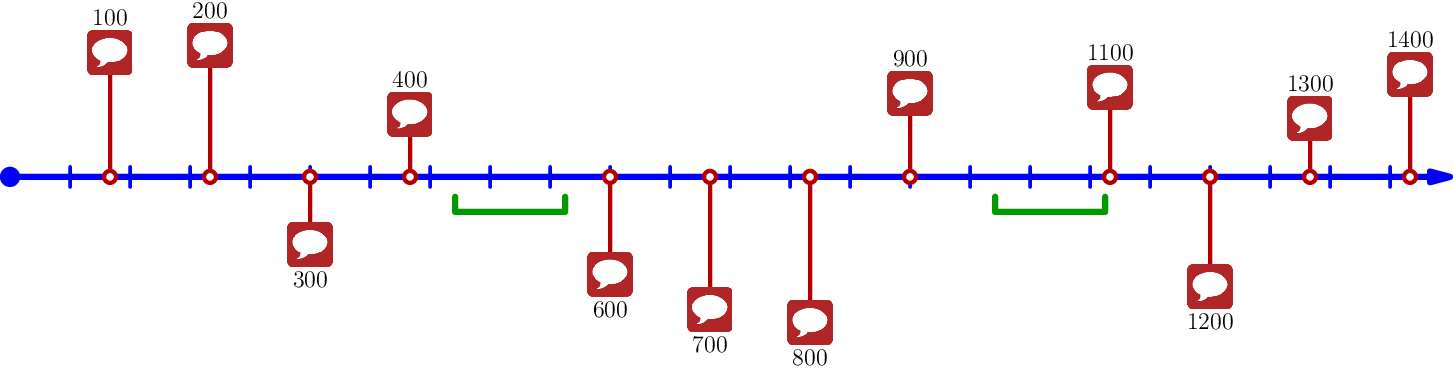:::align{center}  ::: In the **third test case**, the times are the same as in the first test case, but $1000$ is missing. The judge could have walked Boy at most once. In the **fourth test case**, Boy could have been walked during the time intervals $[739, 859]$ and $[859, 979]$. :::align{center}  :::
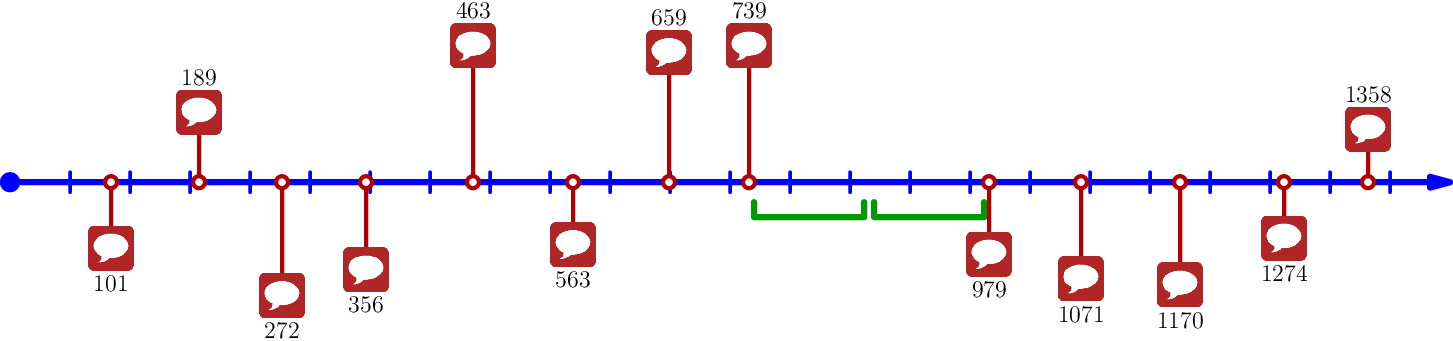